题目内容
设函数g(x)=2(x2+ax)sin
(x∈[0,2],a≥-2)的值域为[-2,0],则实数a的值为 .
| πx |
| 2 |
考点:三角函数的最值
专题:三角函数的图像与性质,不等式的解法及应用
分析:根据sin
的取值范围,将-2≤g(x)≤0,化简
≤2(x2+ax)≤0.即-
-x≤a≤-x.再利用x∈[0,2],即可求得a=-2.
| πx |
| 2 |
| -2 | ||
sin
|
| 1 | ||
xsin
|
解答:
解:∵g(x)=2(x2+ax)sin
,
∴当x=0或x=2时,g(x)=0.
∵当0<x<2时,0<sin
≤1.
∴-2≤g(x)≤0,可化简为
≤2(x2+ax)≤0.
即-
-x≤a≤-x.
又∵x∈[0,2],
∴-x≥-2.
∴a≤-2.
又∵a≥-2,
∴a=-2.
故答案为:-2.
| πx |
| 2 |
∴当x=0或x=2时,g(x)=0.
∵当0<x<2时,0<sin
| πx |
| 2 |
∴-2≤g(x)≤0,可化简为
| -2 | ||
sin
|
即-
| 1 | ||
xsin
|
又∵x∈[0,2],
∴-x≥-2.
∴a≤-2.
又∵a≥-2,
∴a=-2.
故答案为:-2.
点评:本题考查三角函数的性质及最值,不等式的解法及应用等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
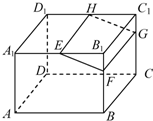 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为