题目内容

设点（a，b）是区域
x-y+1≥0
0≤x≤1
y≥0
内的随机点，则满足a2+b2≤1的概率是
 
．
考点：几何概型,简单线性规划
专题：概率与统计
分析：作出不等式组对应的平面区域，利用几何概型的概率公式进行计算即可得到结论．
解答： 解：作出不等式组对应的平面区域如图：
当x=1时，y=2，即B（1，2），A（1，0），C（0，1），
则四边形OABC的面积S=
1+2
2
×1=
3
2
，
则第一象限内对应a2+b2≤1的面积为
1
4
π，
∴根据几何概型的概率公式可得满足a2+b2≤1的概率是
π
4
3
2
=
π
6
，
故答案为：
π
6
点评：本题主要考查几何概型的概率的计算，求出对应的区域面积是解决本题的关键．
练习册系列答案
相关题目
有一种新型的洗衣液，特点是去污速度快．已知每投放a（1≤a≤4，且a∈R）个单位的洗衣液，它在水中释放的浓度y与时间x（小时）的关系可近似地表示为：y=a•f（x），其中f（x）=
2-
x
6
-
6
x+3
    0≤x＜3
1-
x
6
              3≤x≤6
；若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和．根据经验，只有当水中洗衣液的浓度不低于
1
3
时，才能起到有效去污的作用．
（Ⅰ） 如果只投放1个单位的洗衣液，则能够维持有效去污作用的时间有多长？
（Ⅱ） 第一次投放1个单位的洗衣液后，当水中洗衣液的浓度减少到
1
3
时，马上再投放1个单位的洗衣液，设第二次投放后水中洗衣液的浓度为g（x），求g（x）的函数解析式及其最大值；
（Ⅲ）若第一次投放2个单位的洗衣液，4小时后再投放a个单位的洗衣液，要使接下来的2小时中能够持续有效去污，试求a的最小值．
在△ABC中，sin2C=
3
sinAsinB+sin2B，a=2
3
b，则角C=
 
．
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则下列结论中正确的序号是
 

（1）函数y=f（x）•g（x）的最小正周期为π．
（2）函数y=f（x）•g（x）的最大值为
1
2
．
（3）函数y=f（x）•g（x）的图象关于点（
π
4
，0）成中心对称      
（4）将函数f（x）的图象向右平移
π
2
个单位后得到函数g（x）的图象．
设a=
∫
π
0
（sinx+cosx）dx，则二项式(a
x
-
1
x
)6的展开式的常数项是
 
．
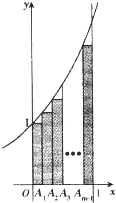如图．A1，A2，…Am-1（m≥2）将区间[0，l]m等分，直线x=0，x=1，y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2．在Ω1中任取一点，则该点取自Ω2的概率等于
 
．
当x∈（0，1）时，不等式x2＜loga（x+1）恒成立，则实数a的范围为
 
．
为了普及环保知识，增强环保意识，某高中随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为
.
x
，则这三个数的大小关系为
 
＜
 
＜
 
．
已知sin2（α+γ）=nsin2β，则
tan(α+β+γ)
tan(α-β+γ)
=（　　）
A、
n-1
n+1
B、
n
n+1
C、
n
n-1
D、
n+1
n-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网