题目内容
若直线（1+a）x+y+1=0与圆x2+y2-2x=0相切，则a的值为（ ）
| A、-1，1 | B、-2，2 |
| C、1 | D、-1 |
考点：圆的切线方程
专题：直线与圆
分析：把圆的方程化为标准形式，根据圆心到直线（1+a）x+y+1=0的距离等于半径，求得a的值．
解答：
解：圆x2+y2-2x=0 即 （x-1）2+y2 =1，表示以（1，0）为圆心、半径等于1的圆，
再根据圆心到直线（1+a）x+y+1=0的距离d=
=1，求得a=-1，
故选：D．
再根据圆心到直线（1+a）x+y+1=0的距离d=
| |1+a+0+1| | ||
|
故选：D．
点评：本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，体现了转化的数学思想，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-| π |
| 2 |
| π |
| 2 |
A、
| ||
B、1+
| ||
C、2+
| ||
D、2
|
如图，在矩形ABCD中，AB=2，AD=已知f（x）=sin（ωx+
），（ω＞0）的图象与y=1的图象的两相邻交点间的距离为π，
要得到y=f（x）的图象，只须把y=sinωx的图象（ ）
| π |
| 3 |
要得到y=f（x）的图象，只须把y=sinωx的图象（ ）
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
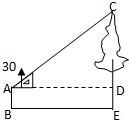如图，小明利用有一个锐角是30°的三角板测量一棵树的高度，已知他与树之间的水平距离BE为5m，AB为1.5m（即小明的眼睛距地面的距离），那么这棵树高是（ ）A、（
| ||||||
B、（5
| ||||||
C、
| ||||||
| D、4m |
已知0＜a＜1，则函数y=|logax|-a|x|零点的个数是（ ）
| A、1个 | B、2个 |
| C、3个 | D、1个或2个或3个 |