题目内容
19.函数f(x)=2x3+x,实数m满足f(m2-2m)+f(m-6)<0,则m的取值范围是(-2,3).分析 根据题意,对函数f(x)=2x3+x求导可得其导数f′(x)=6x2+1>0,分析可得函数f(x)为增函数,进而由f(-x)=-2x3-x=-f(x)分析可得,f(x)为奇函数;结合函数的奇偶性与单调性,可以将f(m2-2m)+f(m-6)<0,转化为m2-2m<6-m,解可得m的取值范围,即可得答案.
解答 解:根据题意,对于函数f(x)=2x3+x,其导数f′(x)=6x2+1>0,则函数f(x)为增函数,
又由f(-x)=-2x3-x=-f(x),则函数f(x)为奇函数,
若f(m2-2m)+f(m-6)<0,
则有f(m2-2m)<-f(m-6),
即f(m2-2m)<f(6-m),
又由函数f(x)为增函数,
则有m2-2m<6-m,
解可得:-2<m<3,
即m的取值范围是(-2,3);
故答案是:(-2,3).
点评 本题考查函数的奇偶性与单调性的综合应用,关键是转化思路,分析函数f(x)的奇偶性与单调性.

练习册系列答案
相关题目
11.O为坐标原点,F为抛物线C:y2=4x的焦点,过F的直线交C于A,B且$\overrightarrow{FA}$=2$\overrightarrow{BF}$,则△OAB的面积为( )
| A. | 4 | B. | $\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2$\sqrt{2}$ |
8.下列说法错误的是( )
| A. | 在△ABC中,若A>B,则cosA<cosB | |
| B. | 若b2=ac,则a,c的等比中项为b | |
| C. | 若命题p与p∧q为真,则q一定为真 | |
| D. | 若p:?x∈(0,+∞),lnx<x-1,则¬p:?x∈(0,+∞),lnx≥x-1 |
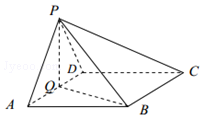 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.