题目内容
9.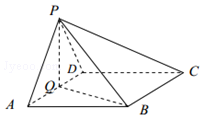 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:AD⊥平面PQB;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P-QBM的体积.
分析 (1)由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;
(2)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC?平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出;
解答 证明:(1)∵PA=PD,
∴PQ⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,
∴BQ⊥AD,PQ∩BQ=Q,
∴AD⊥平面PQB
解:(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,
∴PQ⊥平面ABCD,BC?平面ABCD,
∴PQ⊥BC,
又BC⊥BQ,QB∩QP=Q,
∴BC⊥平面PQB,
又PM=3MC,
∴VP-QBM=VM-PQB=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\sqrt{3}×\frac{3}{4}×2=\frac{3}{4}$.
点评 本题考查几何体的体积的求法,直线与平面垂直的判断与证明,考查空间想象能力以及计算能力,转化思想的应用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
4.已知a=2${\;}^{\frac{4}{3}}$,b=3${\;}^{\frac{2}{3}}$,c=2.5${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | c<a<b |
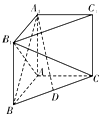 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.