题目内容
若直线
+
=1(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则ab的取值范围是( )
| x |
| a |
| y |
| b |
A、(-∞,
| ||
B、(0,
| ||
| C、(0,8] | ||
| D、[8,+∞) |
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意可得圆心(2,1)在直线
+
=1上,即
+
=1.根据ab=ab(
+
)=2b+a≥2
,由此解一元二次不等式求得ab的范围.
| x |
| a |
| y |
| b |
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
| 2ab |
解答:
解:圆x2+y2-4x-2y-8=0,即(x-2)2+(y-1)2=13,表示以(2,1)为圆心,半径等于
的圆.
∵直线
+
=1(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,
∴故圆心(2,1)在直线
+
=1上,即
+
=1.
∴ab=ab(
+
)=2b+a≥2
,
即
(
-2
)≥0,
即
≥2
,解得 ab≥8,当且仅当
=
时,等号成立,
故选:D.
| 13 |
∵直线
| x |
| a |
| y |
| b |
∴故圆心(2,1)在直线
| x |
| a |
| y |
| b |
| 2 |
| a |
| 1 |
| b |
∴ab=ab(
| 2 |
| a |
| 1 |
| b |
| 2ab |
即
| ab |
| ab |
| 2 |
即
| ab |
| 2 |
| 2 |
| a |
| 1 |
| b |
故选:D.
点评:本题主要考查直线和圆相交的性质,基本不等式的应用,一元二次不等式的解法,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
函数f(x)=0的导数为( )
| A、0 | B、1 | C、不存在 | D、不确定 |
读程序:
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是( )的值.
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是( )的值.
| A、1+2+3+…+99 |
| B、1+2+3+…+100 |
| C、1+(1+2)+(1+2+3)+…+(1+2+3+…+99) |
| D、1+(1+2)+(1+2+3)+…+(1+2+3+…+100) |
在△ABC中,已知a=3,c=3
,A=30°,则角C等于( )
| 3 |
| A、30° | B、60°或120° |
| C、60° | D、120° |
已知复数z满足z•(1-i)=3+i,i为虚数单位,则|z|=( )
A、
| ||
B、
| ||
| C、5 | ||
| D、3 |
设x,y∈R,条件甲:
+
≤1,条件乙:
,则条件甲是条件乙的( )
| x2 |
| 25 |
| y2 |
| 9 |
|
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
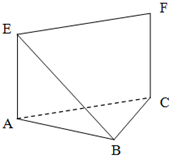 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.