题目内容
等比数列{an}中a1=3，a4=24，则a3+a4+a5=（ ）
| A、33 | B、72 | C、84 | D、189 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据a1=3，a4=24求出数列的公比，从而可求出a3+a4+a5的值．
解答：
解：∵等比数列的通项公式为an=a1qn-1，
∴a4=a1q3=3q3=24，
解得q=2，
∴a3+a4+a5=3q2+3q3+3q4=84，
故选：C．
∴a4=a1q3=3q3=24，
解得q=2，
∴a3+a4+a5=3q2+3q3+3q4=84，
故选：C．
点评：本题主要考查了等差数列的通项公式，利用等比数列性质的能力，同时考查了运算求解的能力，属于基础题．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
已知变量x，y满足约束条件
，则x+y的最大值是（ ）
|
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
下列命题是真命题的是（ ）
| A、梯形一定是平面图形 |
| B、空间中两两相交的三条直线确定一个平面 |
| C、一条直线和一个点能确定一个平面 |
| D、空间中不同三点确定一个平面 |
下列说法中，正确的是（ ）
| A、命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
| B、命题“p或q”为真命题，则命题“p”和命题“q”均为真命题 |
| C、命题“?x∈R，x2-x＞0”的否定是：“?x∈R，x2-x≤0” |
| D、已知x∈R，则“x＞1”是“x＞2”的充分不必要条件 |
z=x-y在
的线性约束条件下，取得最大值的可行解为（ ）
|
| A、（0，1） | ||||
| B、（-1，-1） | ||||
| C、（1，0） | ||||
D、（
|
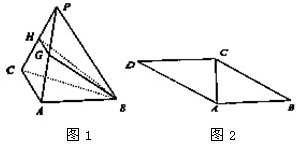已知平行四边形ABCD （如图1）中，AB=4，BC=5，对角线AC=3，将三角形△ACD沿AC折起至△PAC位置（图2），使二面角P-AC-B为60°，G，H分别是PA，PC的中点．