��Ŀ����
��������������
�١�?x��R��3x��5���ķ��ǡ�?x��R��3x��5����
�����⡰����f��x�� ��x=x0���м�ֵ����f�䣨x0��=0���ķ������������⣻
���ڡ�ABC�У�D��BC�е㣬��
•
=
(a2-ac)����B=
��
�ܶ�����R�ϵĺ���y=f��x������f��5+x��=f��-x����(x-
)f��(x)��0����֪x1��x2����f��x1����f��x2����x1+x2��5�ij�Ҫ������
����������ȷ�ĸ����ǣ�������
�١�?x��R��3x��5���ķ��ǡ�?x��R��3x��5����
�����⡰����f��x�� ��x=x0���м�ֵ����f�䣨x0��=0���ķ������������⣻
���ڡ�ABC�У�D��BC�е㣬��
| AD |
| BC |
| 1 |
| 2 |
| �� |
| 3 |
�ܶ�����R�ϵĺ���y=f��x������f��5+x��=f��-x����(x-
| 5 |
| 2 |
����������ȷ�ĸ����ǣ�������
| A��1 | B��2 | C��3 | D��4 |
���㣺���������ж���Ӧ��
ר�⣺�������ۺ�Ӧ��,ƽ��������Ӧ��,������
��������д���س�����ķ��ж��������ȷ��
��д������ķ����⣬����˵��������Ϊ�����⣬�Ӷ�˵��������Ǽ����⣻
�۰�����
��
�û���
��
��ʾ����������ģ��õ�a��b��c�Ĺ�ϵ��Ȼ���������Ҷ������B��
��������Գ��ᣬȻ�����(x-
)f��(x)��0�����ж������ڶԳ�������ĵ����ԣ������ݺ����ĵ����Կ���֤�dz�Ҫ������
��д������ķ����⣬����˵��������Ϊ�����⣬�Ӷ�˵��������Ǽ����⣻
�۰�����
| AD |
| BC |
| AB |
| AC |
��������Գ��ᣬȻ�����(x-
| 5 |
| 2 |
���
�⣺���ڢ٣���?x��R��3x��5���ķ��ǡ�?x��R��3x��5����
�������ȷ��
���ڢڣ����⡰����f��x����x=x0���м�ֵ����f�䣨x0��=0���ķ������ǣ�
������f��x����x=x0����ֵ����f�䣨x0����0����Ϊ�����⣬��f��x��=x3��x=0����ֵ����f�䣨0��=0��
������ڴ���
���ڢۣ���ͼ��
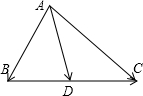
��
•
=
(a2-ac)����
(
+
)•(
-
)=
(a2-ac)��
��
2-
2=a2-ac����b2-c2=a2-ac��
��cosB=
=
=
��
��B=
��
�������ȷ��
���ڢܣ���f��5+x��=f��-x����
�ຯ��f��x������x=
�Գƣ�
��(x-
)f��(x)��0��
��x��
ʱ��f'��x����0������f��x������������
��x��
ʱ��f'��x����0������f��x�������ݼ���
��x1��x2ʱ����f��x1����f��x2��������x1��x2��5-x1��
��x1+x2��5��������������֣�
��x1+x2��5ʱ������x2��5-x1������
�֡�x1��x2��
��f��x1����f��x2���������ʱ�Ҫ��
��f��x1����f��x2����x1+x2��5�ij�Ҫ������
�������ȷ��
����ȷ����ĸ�����3��
�ʴ�Ϊ��3��
�������ȷ��
���ڢڣ����⡰����f��x����x=x0���м�ֵ����f�䣨x0��=0���ķ������ǣ�
������f��x����x=x0����ֵ����f�䣨x0����0����Ϊ�����⣬��f��x��=x3��x=0����ֵ����f�䣨0��=0��
������ڴ���
���ڢۣ���ͼ��

��
| AD |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB |
| 1 |
| 2 |
��
| AC |
| AB |
��cosB=
| a2+c2-b2 |
| 2ac |
| ac |
| 2ac |
| 1 |
| 2 |
��B=
| �� |
| 3 |
�������ȷ��
���ڢܣ���f��5+x��=f��-x����
�ຯ��f��x������x=
| 5 |
| 2 |
��(x-
| 5 |
| 2 |
��x��
| 5 |
| 2 |
��x��
| 5 |
| 2 |
��x1��x2ʱ����f��x1����f��x2��������x1��x2��5-x1��
��x1+x2��5��������������֣�
��x1+x2��5ʱ������x2��5-x1������
�֡�x1��x2��
��f��x1����f��x2���������ʱ�Ҫ��
��f��x1����f��x2����x1+x2��5�ij�Ҫ������
�������ȷ��
����ȷ����ĸ�����3��
�ʴ�Ϊ��3��
���������⿼�����������ж���Ӧ�ã������˺����ĵ����뼫ֵ��Ĺ�ϵ��ѵ�������õ������ķ����ж�ԭ�����ĵ����ԣ�ѵ����ƽ�������ڽ��������е�Ӧ�ã����е��⣮

��ϰ��ϵ�д�
 �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ
����������ȷ���У�������
��1����С��ʵ�����Թ��ɼ��ϣ�
��2������{y|y=x2-1}�뼯��{t|t=x2-1}��ͬһ�����ϣ�
��3��1��
��
��|-
|��0.5��Щ����ɵļ�����5��Ԫ�أ�
��4��y=
�ļ�����Ϊ��-�ޣ�0���ȣ�0��+�ޣ���
��1����С��ʵ�����Թ��ɼ��ϣ�
��2������{y|y=x2-1}�뼯��{t|t=x2-1}��ͬһ�����ϣ�
��3��1��
| 3 |
| 2 |
| 6 |
| 4 |
| 1 |
| 2 |
��4��y=
| 1 |
| x |
| A��0�� | B��1�� | C��2�� | D��3�� |
�ȱ�����{an}��a1=3��a4=24����a3+a4+a5=��������
| A��33 | B��72 | C��84 | D��189 |
��������y2=2px��p��0�������ֱ�߽���������A��B���㣬��|AB|����СֵΪ��������
A��
| ||
| B��p | ||
| C��2p | ||
| D����ȷ�� |
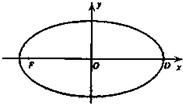 ��֪��ƽ��ֱ������ϵxOy�е�һ����ԲC������������ԭ�㣬��Ϊ
��֪��ƽ��ֱ������ϵxOy�е�һ����ԲC������������ԭ�㣬��Ϊ