题目内容
有下列命题:
①在函数y=cos(x-
)cos(x+
)的图象中,相邻两个对称中心的距离为π;
②函数y=
的图象关于点(-1,1)对称;
③关于x的方程ax2-2ax-1=0有且仅有一个实数根,则实数a=-1;
④在△ABC中,若3sinA+4cosB=6,4sinB+3cosA=1,则角C等于30°或150°.
其中所有真命题的序号是 .
①在函数y=cos(x-
| π |
| 4 |
| π |
| 4 |
②函数y=
| x+3 |
| x-1 |
③关于x的方程ax2-2ax-1=0有且仅有一个实数根,则实数a=-1;
④在△ABC中,若3sinA+4cosB=6,4sinB+3cosA=1,则角C等于30°或150°.
其中所有真命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用诱导公式和倍角公式、周期公式即可得出;
②函数变形为y=
=1+
,即可得出图象关于点(1,1)对称;
③对a分类讨论:当a≠0时,由△=0,解得a,当a=0时,直接验证即可;
④利用平方关系和两角和的正弦公式、诱导公式、三角形的内角和定理即可得出.
②函数变形为y=
| x+3 |
| x-1 |
| 4 |
| x-1 |
③对a分类讨论:当a≠0时,由△=0,解得a,当a=0时,直接验证即可;
④利用平方关系和两角和的正弦公式、诱导公式、三角形的内角和定理即可得出.
解答:
解:①y=cos(x-
)cos(x+
)=sin(x+
)cos(x+
)=
sin(2x+
)=
cos2x,
∴T=
=π,∴图象相邻两个对称中心的距离为
,因此不正确;
②函数y=
=1+
的图象关于点(1,1)对称,因此②不正确;
③关于x的方程ax2-2ax-1=0有且仅有一个实数根,
当a=0时,不适合;
当a≠0时,由△=4a2+4a=0,解得a=-1.
综上可知:实数a=-1,因此正确;
④在△ABC中,由3sinA+4cosB=6,4sinB+3cosA=1,
分别平方相加可得9+16+24sin(A+B)=37,
化为sinC=
,则角C等于30°或150°.因此正确.
综上可知:只有③④正确.
故答案为:③④.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∴T=
| 2π |
| 2 |
| π |
| 2 |
②函数y=
| x+3 |
| x-1 |
| 4 |
| x-1 |
③关于x的方程ax2-2ax-1=0有且仅有一个实数根,
当a=0时,不适合;
当a≠0时,由△=4a2+4a=0,解得a=-1.
综上可知:实数a=-1,因此正确;
④在△ABC中,由3sinA+4cosB=6,4sinB+3cosA=1,
分别平方相加可得9+16+24sin(A+B)=37,
化为sinC=
| 1 |
| 2 |
综上可知:只有③④正确.
故答案为:③④.
点评:本题综合考查了三角函数的平方关系、两角和的正弦公式、诱导公式、三角形的内角和定理、函数的对称性、一元二次方程的实数根与判别式的关系等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
等比数列{an}中a1=3,a4=24,则a3+a4+a5=( )
| A、33 | B、72 | C、84 | D、189 |
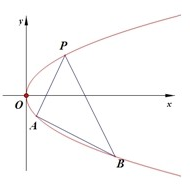 如图,抛物线的方程为y2=2px(p>0).
如图,抛物线的方程为y2=2px(p>0).