题目内容
设T={(x,y)|ax+y-3=0},S={(x,y)|x-y-b=0}.若S∩T={(2,1)},则a= ,b= .
考点:交集及其运算
专题:集合
分析:由S∩T={(2,1)}知,(2,1)是集合S与T的公共元素,将x=2,y=1分别代入两方程中即得a,b的值.
解答:
解:由S∩T={(2,1)},知(2,1)∈T,(2,1)∈S,
在集合T中,将x=2,y=1代入ax+y-3=0中得2a+1-3=0,得a=1,
在集合S中,将x=2,y=1代入x-y-b=0中得2-1-b=0,得b=1.
故答案为1,1.
在集合T中,将x=2,y=1代入ax+y-3=0中得2a+1-3=0,得a=1,
在集合S中,将x=2,y=1代入x-y-b=0中得2-1-b=0,得b=1.
故答案为1,1.
点评:1.求解集合问题时,一般先要弄清用描述法表示的集合中,元素的代表符号和属性(如元素是点还是数),再进行其他相关运算.
2.对于点集,常运用数形结合思想,考虑点集表示的图形是什么,进行交集运算时,交集是两图形的公共点组成的集合,从而将“交”的运算转化为解方程组的问题.
2.对于点集,常运用数形结合思想,考虑点集表示的图形是什么,进行交集运算时,交集是两图形的公共点组成的集合,从而将“交”的运算转化为解方程组的问题.

练习册系列答案
相关题目
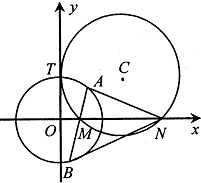 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3. 某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为
某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为
