题目内容
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.考点:异面直线及其所成的角
专题:空间角
分析:利用平行线法找到异面直线所成的角,∠DB1B即异面直线DB1与CC1所成的角,然后放在三角形中计算.
解答:
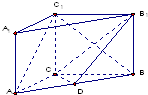 解:直三棱柱ABC-A1B1C1中CC1∥BB1
解:直三棱柱ABC-A1B1C1中CC1∥BB1
所以∠DB1B为异面直线DB1与CC1所成的角(或其补角) (3分)
直三棱柱ABC-A1B1C1中
VB1-BCD=
S△BCD•B1B=
×
×4×
B1B=2得BB1=2 (7分)
由点D是AB的中点得DB=
直三棱柱ABC-A1B1C1中B1B⊥BD
Rt△B1BD中tan∠DB1B=
=
=
所以∠DB1B=arctan
(或∠DB1B=arccos
)
所以异面直线DB1与BC1所成的角为arctan
(或arccos
) (12分)
 解:直三棱柱ABC-A1B1C1中CC1∥BB1
解:直三棱柱ABC-A1B1C1中CC1∥BB1所以∠DB1B为异面直线DB1与CC1所成的角(或其补角) (3分)
直三棱柱ABC-A1B1C1中
VB1-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
由点D是AB的中点得DB=
| 5 |
| 2 |
直三棱柱ABC-A1B1C1中B1B⊥BD
Rt△B1BD中tan∠DB1B=
| BD |
| B1B |
| ||
| 2 |
| 5 |
| 4 |
所以∠DB1B=arctan
| 5 |
| 4 |
| 4 |
| 41 |
| 41 |
所以异面直线DB1与BC1所成的角为arctan
| 5 |
| 4 |
| 4 |
| 41 |
| 41 |
点评:本题考查异面直线所成的角的计算,先作后求是基本方法.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=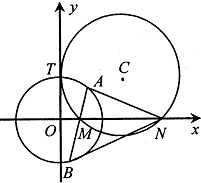 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.