题目内容
已知f(x)为定义在R上奇函数,当满足x≤y且xy≠0时有f(x+y)=3f(x)+4f(y)+3x2-5y2+2x+3y+1,求f(x)的表达式.
考点:抽象函数及其应用,函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质,以及抽象函数的表达式,利用赋值法即可得到结论.
解答:
解:∵f(x)为定义在R上奇函数,
∴f(0)=0,
∵当满足x≤y且xy≠0时有f(x+y)=3f(x)+4f(y)+3x2-5y2+2x+3y+1,
∴令y=-x,若x≤y且,xy≠0,
则x≤-x,且x≠0,y≠0,此时x<0,
则f(x-x)=3f(x)+4f(-x)+3x2-5(-x)2+2x+3(-x)+1=f(0)=0,
则3f(x)-4f(x)-2x2-x+1=0,
则f(x)=-2x2-x+1,
若x>0,则-x<0,
则f(-x)=-2x2+x+1,
∵f(x)是奇函数,∴f(-x)=-2x2+x+1=-f(x),
则f(x)=2x2-x-1,x>0.
故函数f(x)=
.
∴f(0)=0,
∵当满足x≤y且xy≠0时有f(x+y)=3f(x)+4f(y)+3x2-5y2+2x+3y+1,
∴令y=-x,若x≤y且,xy≠0,
则x≤-x,且x≠0,y≠0,此时x<0,
则f(x-x)=3f(x)+4f(-x)+3x2-5(-x)2+2x+3(-x)+1=f(0)=0,
则3f(x)-4f(x)-2x2-x+1=0,
则f(x)=-2x2-x+1,
若x>0,则-x<0,
则f(-x)=-2x2+x+1,
∵f(x)是奇函数,∴f(-x)=-2x2+x+1=-f(x),
则f(x)=2x2-x-1,x>0.
故函数f(x)=
|
点评:本题主要考查函数解析式的求解,根据函数的奇偶性以及赋值法是解决本题的关键.

练习册系列答案
相关题目
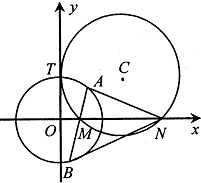 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.