题目内容
2. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD(1)求证:AD⊥PB;
(2)若BD与平面PBC的所成角为30°,求三棱锥P-BCD的体积.
分析 (1)由余弦定理得BD2=3,从而AB2=AD2+BD2,进而AD⊥BD,由PD⊥平面ABCD,得PD⊥AD,由此能证明AD⊥平面PBD,从而AD⊥PB.
(2)过D作DE⊥PB,垂足为E,推导出BC⊥平面PBD,从而DE⊥平面PBC,由此能求出三棱锥P-BCD的体积.
解答 证明:(1)在△ABD中,∠DAB=60°,AB=2AD=2,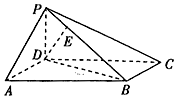
由余弦定理得BD2=AB2+AD2-2AB•ADcos∠DAB=3,
∴AB2=AD2+BD2,∴∠ADB=90°,
∴AD⊥BD,
∵PD⊥平面ABCD,∴PD⊥AD,
∴AD⊥平面PBD,∴AD⊥PB.
解:(2)过D作DE⊥PB,垂足为E,
∵ABCD是平行四边形,∴AD∥BC,
∴由(1)得AD⊥平面PBD,∴BC⊥平面PBD,
∴平面PBC⊥平面PBD,∴DE⊥平面PBC,
∴BD与平面PBC所成角为∠DBE=30°,
由(1)得BD=$\sqrt{3}$,DP=BD•tan∠DBE=1,
∴三棱锥P-BCD的体积:
${V}_{P-BCD}=\frac{1}{3}{S}_{△BCD}•DP=\frac{1}{3}×\frac{1}{2}×BD×BC×DP$=$\frac{\sqrt{3}}{6}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
10.已知等差数列{an},a1=-2013,其n前项和${S_n},若\frac{{{S_{12}}}}{12}-\frac{{{S_{10}}}}{10}=2,则{S_{2017}}$=( )
| A. | 2017 | B. | 3 | C. | 6051 | D. | -2017 |
7.已知集合A={k∈N|$\sqrt{10-K}$∈N},B={x|x=2n或x=3n,n∈N},则A∩B=( )
| A. | {6,9} | B. | {3,6,9} | C. | {1,6,9,10} | D. | {6,9,10} |
12.已知数列{an}的前n项和是Sn,且满足an+3Sn•Sn-1=0(n≥2),若${S_6}=\frac{1}{20}$,则a1=( )
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | 5 | D. | 1 |
 如图四棱椎P-ABCD中,四边形ABCD是矩形,平面PAD⊥平面ABCD,其中M,N分别是PD,BC的中点
如图四棱椎P-ABCD中,四边形ABCD是矩形,平面PAD⊥平面ABCD,其中M,N分别是PD,BC的中点