题目内容
若方程ax2-x-1=0在区间（0，1）内恰有一个解，则实数a的取值范围是 ．
考点：二分法求方程的近似解
专题：计算题,函数的性质及应用
分析：讨论a的不同取值以确定方程是否是二次方程及二次方程的根的大致位置，再由方程的根与函数的零点的关系判断即可．
解答：
解：若a=0，则方程ax2-x-1=0的解为-1，不成立；
若a＜0，则方程ax2-x-1=0不可能有正根，故不成立；
若a＞0，则△=1+4a＞0，且c=-1＜0；
故方程有一正一负两个根，
故方程ax2-x-1=0在区间（0，1）内恰有一个解可化为
（a•02-0-1）（a•12-1-1）＜0；
解得，a＞2；
故答案为：a＞2．
若a＜0，则方程ax2-x-1=0不可能有正根，故不成立；
若a＞0，则△=1+4a＞0，且c=-1＜0；
故方程有一正一负两个根，
故方程ax2-x-1=0在区间（0，1）内恰有一个解可化为
（a•02-0-1）（a•12-1-1）＜0；
解得，a＞2；
故答案为：a＞2．
点评：本题考查了方程的根的判断及分类讨论的数学思想应用，属于基础题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
若集合A={x|x2-2x-16≤0}，B={x|C5x≤5}，则A∩B中元素个数为]（ ）
| A、4个 | B、6个 | C、2个 | D、0个 |
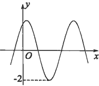如图，函数f（x）=Asin（2x+φ）（A＞0，|φ|＜| π |
| 2 |
| 3 |
A、（-
| ||
B、（-
| ||
C、（
| ||
D、（
|
数列{an}中，a1=1，a2n=n-an，a2n+1=an+1，则a100=（ ）
| A、30 | B、31 | C、32 | D、33 |