题目内容
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为5的样本,问样本中看与不看营养说明的女生各有多少名?
(2)根据列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
| 男 | 女 | 总计 | |||||||||||||
| 看营养说明 | 50 | 30 | 80 | ||||||||||||
| 不看营养说明 | 10 | 20 | 30 | ||||||||||||
| 总计 | 60 | 50 | 110 | ||||||||||||
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |||||
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||||
(2)根据列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据分层抽样可得样本中看与不看营养说明的女生人数;
(2)利用公式求得K2,与临界值比较,即可得到结论.
(2)利用公式求得K2,与临界值比较,即可得到结论.
解答:
解:(1)根据分层抽样可得:样本中看营养说明的女生有
×30=3名,样本中不看营养说明的女生有
×20=2名;
(2)假设H0:该校高中学生性别与在购买食物时看营养说明无关,则K2应该很小.
根据题中的列联表得k=
=
≈7.486
由P(K2≥6.635)=0.010,P(K2≥7.879)=0.005可知
有99%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关
| 5 |
| 50 |
| 5 |
| 50 |
(2)假设H0:该校高中学生性别与在购买食物时看营养说明无关,则K2应该很小.
根据题中的列联表得k=
| 110×(50×20-30×10)2 |
| 80×30×60×50 |
| 539 |
| 72 |
由P(K2≥6.635)=0.010,P(K2≥7.879)=0.005可知
有99%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关
点评:本题考查分层抽样,考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
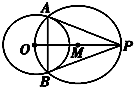 如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.
如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.