题目内容
20．已知f（x）=|x|（2-x）（1）作出函数f（x）的大致图象，并指出其单调区间；
（2）若函数f（x）=c恰有三个不同的解，试确定实数c的取值范围．
分析 （1）化简函数的表达式，然后画出函数的图象，写出单调区间即可．
（2）利用函数的图象，推出实数c的取值范围．
解答 解：（1）f（x）=|x|（2-x）=$\left\{\begin{array}{l}{2x-{x}^{2}，x≥0}\\{{x}^{2}-2x，x＜0}\end{array}\right.$，函数的图象如图：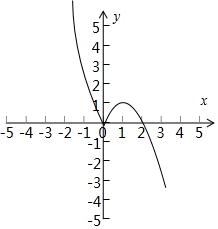
函数的单调增区间（0，1），单调减区间（-∞，0），（1，+∞）．
（2）函数f（x）=c恰有三个不同的解，函数在x=1时取得极大值：1，
实数c的取值范围（0，1）．
点评 本题考查分段函数的应用，函数的图象以及函数的零点个数的判断，考查数形结合以及计算能力．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
10．
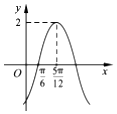函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）| A． | $f（x）=2sin（{x-\frac{π}{6}}）$ | B． | $f（x）=2sin（{2x-\frac{π}{3}}）$ | C． | $f（x）=2sin（{x+\frac{π}{12}}）$ | D． | $f（x）=2sin（{2x-\frac{π}{6}}）$ |
11．某班50人的一次竞赛成绩的频数分布如下：[60，70）：3人，[70，80）：16人，[80，90）：24人，[90，100]：7人，利用各组区间中点值，可估计本次比赛该班的平均分为（ ）
| A． | 56 | B． | 68 | C． | 78 | D． | 82 |
15．设集合M=[0，$\frac{1}{2}$），N=[$\frac{1}{2}$，1]，函数f（x）=$\left\{\begin{array}{l}{x+\frac{1}{2}，x∈M}\\{2（1-x），x∈N}\end{array}\right.$．若x0∈M且f（f（x0））∈M，则x0的取值范围为（ ）
| A． | （0，$\frac{1}{4}$] | B． | [0，$\frac{3}{8}$] | C． | （$\frac{1}{4}$，$\frac{1}{2}$] | D． | （$\frac{1}{4}$，$\frac{1}{2}$） |
12．给定空间中的直线l与平面α，则“直线l与平面α垂直”是“直线l垂直于平面α上无数条直线”的（ ）条件．
| A． | 充分非必要 | B． | 必要非充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |