题目内容

5．函数f（x）=2x+m的反函数为y=f-1（x），且y=f-1（x）的图象过点Q（5，2），那么m=1．

分析 根据反函数的性质可知：原函数与反函数的图象关于y=x对称，利用对称关系可得答案．

解答 解：f（x）=2x+m的反函数y=f-1（x），
∵函数y=f-1（x）的图象经过Q（5，2），原函数与反函数的图象关于y=x对称，
∴f（x）=2x+m的图象经过Q′（2，5），
即4+m=5，
解得：m=1．
故答案为：1．

点评 本题考查了原函数与反函数的图象的关系，它们的图象关于y=x对称，即坐标也对称．属于基础题．

练习册系列答案
相关题目
15．${（{x^3}+\frac{1}{{\sqrt{x}}}）^n}$的展开式的所有二项式系数之和为128，则n为（　　）
A．5B．6C．7D．8
16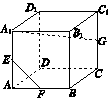．如图所示，在正方体ABCD-A1B1C1D1中，AA1，AB，CC1的中点分别为E，F，G，则EF与A1G所成的角为（　　）
A．30°B．45°C．60°D．90°
13．下列函数中，在其定义域既是奇函数又是减函数的是（　　）
A．y=|x|B．y=-x3C．y=（$\frac{1}{2}$）xD．y=$\frac{1}{x}$
20．已知f（x）=|x|（2-x）
（1）作出函数f（x）的大致图象，并指出其单调区间；
（2）若函数f（x）=c恰有三个不同的解，试确定实数c的取值范围．
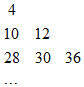10．设数列{an}是集合{x|x=3s+3t，s＜t且s，t∈N}中所有的数从小到大排列成的数列，即a1=4，a2=10，a3=12，a4=28，a5=30，a6=36，…，将数列{an}中各项按照上小下大，左小右大的原则排成如图的等腰直角三角形数表，则a15的值为324．
17．已知函数g（x）=ax2-2ax+1+b（a＞0）在区间[2，3]上的最大值为4，最小值为1，记f（x）=g（|x|），x∈R；
（1）求实数a、b的值；
（2）若不等式$f（x）+g（x）≥log_2^2k-2{log_2}k-3$对任意x∈R恒成立，求实数k的范围；
（3）对于定义在[p，q]上的函数m（x），设x0=p，xn=q，用任意xi（i=1，2，…，n-1）将[p，q]划分成n个小区间，其中xi-1＜xi＜xi+1，若存在一个常数M＞0，使得不等式|m（x0）-m（x1）|+|m（x1）-m（x2）|+…+|m（xn-1）-m（xn）|≤M恒成立，则称函数m（x）为在[p，q]上的有界变差函数，试证明函数f（x）是在[1，3]上的有界变差函数，并求出M的最小值．
14．如图所示，沿河有A、B两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污
水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为f（m）=25•m0.7（万元），m表示污水流量，铺设管道的费用（包括管道费）$g（x）=3.2\sqrt{x}$（万元），x表示输送污水管道的长度（千米）；
已知城镇A和城镇B的污水流量分别为m1=3、m2=5，A、B两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）
（1）若在城镇A和城镇B单独建厂，共需多少总费用？
（2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为x千米，求联合建厂的总费用y与x的函数关系
式，并求y的取值范围．
4．已知△ABC中，三条边a，b，c所对的角分别为A、B、C，且a2+b2-c2=ab
（Ⅰ）求角C的大小；
（Ⅱ）若f（x）=$\sqrt{3}$sinxcosx+cos2x，求f（B）的最大值，并判断此时△ABC$；\\;的$的形状．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网