题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若f(f(a))=2,则实数a的值为-$\sqrt{3}$,$\frac{1}{2}$,16.分析 f(f(a))=2,由此利用分类讨论思想能求出a.
解答 解:由f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,f(f(a))=2,
当log2a≤0时,即0<a≤1时,(log2a)2+1=2,
即(log2a)2=1,
解得a=$\frac{1}{2}$,
当log2a>0时,即a>1时,log2(log2a)=2,
解得a=16,
因为a2+1>0,log2(a2+1)=2,即a2+1=4
解得a=$\sqrt{3}$(舍去),或-$\sqrt{3}$,
综上所述a的值为-$\sqrt{3}$,$\frac{1}{2}$,16,
故答案为:-$\sqrt{3}$,$\frac{1}{2}$,16,
点评 本题考查函数值的求法及应用,是中档题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
相关题目
18.已知双曲线$E:{x^2}-\frac{y^2}{3}=1$的左焦点为F,直线x=2与双曲线E相交于A,B两点,则△ABF的面积为( )
| A. | 12 | B. | 24 | C. | $4\sqrt{3}$ | D. | $8\sqrt{3}$ |
16.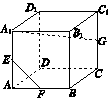 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
13.下列函数中,在其定义域既是奇函数又是减函数的是( )
| A. | y=|x| | B. | y=-x3 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{x}$ |