题目内容

9．已知两个不相等的非零向量$\overrightarrow a$和$\overrightarrow b$，向量组$（\overrightarrow{x_1}，\overrightarrow{x_2}，\overrightarrow{x_3}，\overrightarrow{x_4}）$和$（\overrightarrow{y_1}，\overrightarrow{y_2}，\overrightarrow{y_3}，\overrightarrow{y_4}）$均由2个$\overrightarrow a$和2个$\overrightarrow b$排列而成，记$S=\overrightarrow{x_1}•\overrightarrow{y_1}+\overrightarrow{x_2}•\overrightarrow{y_2}+\overrightarrow{x_3}•\overrightarrow{y_3}+\overrightarrow{x_4}•\overrightarrow{y_4}$，那么S的所有可能取值中的最小值是$4\overrightarrow{a}•\overrightarrow{b}$（用向量$\overrightarrow a$、$\overrightarrow b$表示）

分析 由题意即可求出S的所有可能的取值，然后根据不等式a2+b2≥2ab及数量积的计算公式即可比较这些值的大小，从而找出最小值．

解答 解：根据条件得，S所有可能取值为：
$2（{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}）$$≥4|\overrightarrow{a}||\overrightarrow{b}|≥4\overrightarrow{a}•\overrightarrow{b}$，${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}≥2|\overrightarrow{a}||\overrightarrow{b}|+2\overrightarrow{a}•\overrightarrow{b}≥4\overrightarrow{a}•\overrightarrow{b}$，
∴S的所有可能取值中的最小值为$4\overrightarrow{a}•\overrightarrow{b}$．
故答案为：$4\overrightarrow{a}•\overrightarrow{b}$．

点评 考查数量积的计算公式，余弦函数的值域，以及不等式a2+b2≥2ab的运用．

练习册系列答案
相关题目
19．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0，c=\sqrt{{a^2}-{b^2}}，e=\frac{c}{a}）$，其左、右焦点分别为F1，F2，关于椭圆有以下四种说法：
（1）设A为椭圆上任一点，其到直线${l_1}：x=-\frac{a^2}{c}，{l_2}：x=\frac{a^2}{c}$的距离分别为d2，d1，则$\frac{{|A{F_1}|}}{d_1}=\frac{{|A{F_2}|}}{d_2}$；
（2）设A为椭圆上任一点，AF1，AF2分别与椭圆交于B，C两点，则$\frac{{|A{F_1}|}}{{|{F_1}B|}}+\frac{{|A{F_2}|}}{{|{F_2}C|}}≥\frac{{2（1+{e^2}）}}{{1-{e^2}}}$（当且仅当点A在椭圆的顶点取等）；
（3）设A为椭圆上且不在坐标轴上的任一点，过A的椭圆切线为l，M为线段F1F2上一点，且$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$，则直线AM⊥l；
（4）面积为2ab的椭圆内接四边形仅有1个．
其中正确的有（　　）个．
A．1B．2C．3D．4
20．已知f（x）=|x|（2-x）
（1）作出函数f（x）的大致图象，并指出其单调区间；
（2）若函数f（x）=c恰有三个不同的解，试确定实数c的取值范围．
17．已知函数g（x）=ax2-2ax+1+b（a＞0）在区间[2，3]上的最大值为4，最小值为1，记f（x）=g（|x|），x∈R；
（1）求实数a、b的值；
（2）若不等式$f（x）+g（x）≥log_2^2k-2{log_2}k-3$对任意x∈R恒成立，求实数k的范围；
（3）对于定义在[p，q]上的函数m（x），设x0=p，xn=q，用任意xi（i=1，2，…，n-1）将[p，q]划分成n个小区间，其中xi-1＜xi＜xi+1，若存在一个常数M＞0，使得不等式|m（x0）-m（x1）|+|m（x1）-m（x2）|+…+|m（xn-1）-m（xn）|≤M恒成立，则称函数m（x）为在[p，q]上的有界变差函数，试证明函数f（x）是在[1，3]上的有界变差函数，并求出M的最小值．
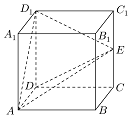4．如图，已知正方形ABCD-A1B1C1D1，AA1=2，E为棱CC1的中点，则三棱锥D1-ADE的体积为$\frac{4}{3}$．
14．如图所示，沿河有A、B两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污
水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为f（m）=25•m0.7（万元），m表示污水流量，铺设管道的费用（包括管道费）$g（x）=3.2\sqrt{x}$（万元），x表示输送污水管道的长度（千米）；
已知城镇A和城镇B的污水流量分别为m1=3、m2=5，A、B两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）
（1）若在城镇A和城镇B单独建厂，共需多少总费用？
（2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为x千米，求联合建厂的总费用y与x的函数关系
式，并求y的取值范围．
1．若矩阵$（\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}）$满足：a11，a12，a21，a22∈{0，1}，且$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|$=0，则这样的互不相等的矩阵共有（　　）
A．2个B．6个C．8个D．10个
18．（1）3${\;}^{1+lo{g}_{3}2}$=6． 
（2）${log_3}\frac{1}{2}+{log_3}\frac{2}{3}+{log_3}\frac{3}{4}+…+{log_3}\frac{80}{81}$=-4．
8．$\root{3}{2{7}^{2}}$-2${\;}^{lo{g}_{2}3}$×log2$\frac{1}{8}$+lg25+2lg2=20．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网