题目内容
5.给出下列四个命题:①两个向量相等,则它们的起点相同,终点相同;
②若$\overrightarrow{a}$=$\overrightarrow{b}$,$\overrightarrow{b}$=$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{c}$;
③设$\overrightarrow{{a}_{0}}$是单位向量,若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$,且|$\overrightarrow{d}$|=1,则$\overrightarrow{d}$=$\overrightarrow{{a}_{0}}$;
④$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$.
其中假命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,两个向量相等,与它们的起点、终点无关,只要方向同,模等即可;
②,根据向量相等的定义判定;
③,设$\overrightarrow{{a}_{0}}$是单位向量,若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$,且|$\overrightarrow{d}$|=1,则$\overrightarrow{d}$与$\overrightarrow{{a}_{0}}$有可能方向不同;
④向量共线,方向不一定同,
解答 解:对于①,两个向量相等,与它们的起点、终点无关,只要方向同,模等即可,故为假命题;
对于②,根据向量相等的定义,若$\overrightarrow{a}$=$\overrightarrow{b}$,$\overrightarrow{b}$=$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{c}$,为真命题;
对于③,设$\overrightarrow{{a}_{0}}$是单位向量,若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$,且|$\overrightarrow{d}$|=1,则$\overrightarrow{d}$与$\overrightarrow{{a}_{0}}$有可能方向不同,故为假命题;
④向量共线,方向不一定同,故$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$|=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$为假命题.
故选:C.
点评 本题考查了命题真假的判定,属于基础题.

 名校课堂系列答案
名校课堂系列答案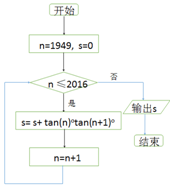
| A. | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B. | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C. | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D. | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
| A. | m>0>n | B. | 0>m>n | ||
| C. | m>n>0 | D. | m,n与0的大小关系不确定 |
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | y2-x2=50 | D. | x2-y2=10 |
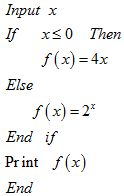
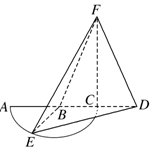 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.