题目内容
20.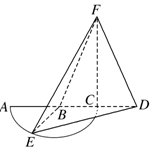 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.(Ⅰ)证明:EB⊥FD;
(Ⅱ)求点B到平面FED的距离.
分析 (Ⅰ)证明:EB⊥平面FBD,即可证明EB⊥FD;
(Ⅱ)在平面FCH内过C作CK⊥FH,则CK⊥平面FED.即可求点B到平面FED的距离.
解答 (Ⅰ)证明:∵FC⊥平面BED,BE?平面BED,∴EB⊥FC.
又点E为$\widehat{AC}$的中点,B为直径AC的中点,∴EB⊥BC.
又∵FC∩BC=C,∴EB⊥平面FBD.
∵FD?平面FBD,∴EB⊥FD.
(Ⅱ)解:如图,在平面BEC内过C作CH⊥ED,连接FH.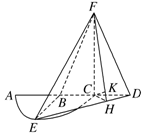
则由FC⊥平面BED知,ED⊥平面FCH.
∵Rt△DHC∽Rt△DBE,∴$\frac{DC}{DE}$=$\frac{CH}{BE}$.
在Rt△DBE中,DE=$\sqrt{B{E}^{2}+B{D}^{2}}$=$\sqrt{5}$,
∴CH=$\frac{DC•BE}{DE}$=$\frac{\sqrt{5}}{5}$.
在平面FCH内过C作CK⊥FH,则CK⊥平面FED.
∵FC=2.∴FH2=FC2+CH2=$\frac{21}{5}$,∴FH=$\frac{\sqrt{105}}{5}$.
∴CK=$\frac{FC•CH}{FH}$=$\frac{2\sqrt{21}}{21}$.
∵C是BD的中点,∴B到平面FED的距离为2CK=$\frac{4\sqrt{21}}{21}$.
点评 本题考查线面平行的判定与性质,考查点到平面距离的计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件A,“第2次拿出的是白球”为事件B,则P(B|A)是( )
| A. | $\frac{5}{8}$ | B. | $\frac{5}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{14}$ |
11.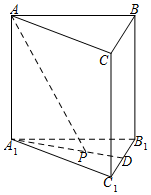 已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
 已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
已知正三棱柱(底面是正三角形,且侧棱与底面垂直的棱柱)ABC-A1B1C1体积为$\frac{9}{4}$,底面边长为$\sqrt{3}$.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
15.已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且$\frac{2x+3}{x}>-\frac{{{f^'}(x)}}{f(x)}$总成立,则下列不等式成立的是( )
| A. | e2e+3f(e)<e2ππ3f(π) | B. | e2e+3f(π)>e2ππ3f(e) | C. | e2e+3f(π)<e2ππ3f(e) | D. | e2e+3f(e)>e2ππ3f(π) |
12.函数f(x)的定义域为R+,且对于任何正实数x、y都有f(xy)=f(x)+f(y),若f(8)=6,则f($\sqrt{2}$)=( )
| A. | 1 | B. | 2 | C. | -1 | D. | $\sqrt{2}$ |
9.已知曲线 f(x)=ax2-2在横坐标为1的点 p处切线的倾斜角为$\frac{π}{4}$,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | -1 |
3.已知函数f(x)=$\left\{\begin{array}{l}{sinx,x≥0}\\{-{x}^{2}-1,x<0}\end{array}\right.$,若f(x)≤kx,则k的范围为( )
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |