题目内容
已知数列{an}中,a1=3,前n项和为Sn,且2Sn=(n+1)an+n-1.
(1)求数列{an}的通项公式;
(2)设bn=
,数列{bn}的前n项和为Tn,若Tn≤M对一切正整数n都成立,求出M的最小值.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| anan+1 |
考点:数列的求和,数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)依题意,2Sn=(n+1)an+n-1⇒2Sn-1=nan-1+n-2,n≥2,两式相减可得(n-1)an-nan-1=-1⇒
-
=
-
(n≥2),利用累加法即可求得
=
+2,继而可得数列{an}的通项公式;
(2)利用裂项法可得bn=
=
=
(
-
),累加求和可得Tn=b1+b2+…+bn=
(
-
)≤M对一切正整数n都成立,从而可求得M的最小值.
| an |
| n |
| an-1 |
| n-1 |
| 1 |
| n |
| 1 |
| n-1 |
| an |
| n |
| 1 |
| n |
(2)利用裂项法可得bn=
| 1 |
| anan+1 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
解答:
解:(1)∵数列{an}中,a1=3,2Sn=(n+1)an+n-1,①
∴2Sn-1=nan-1+n-2,n≥2,②
①-②,得:2an=(n+1)an-nan-1+1,n≥2.
∴(n-1)an-nan-1=-1,
∴
-
=-
=
-
(n≥2),
∴(
-
)+(
-
)+…+(
-
)=(
-
)+(
-
)+…+(
-1),
即
-
=
-1,∵a1=3,
∴
=
+2,
∴an=2n+1.
(2)∵bn=
=
=
(
-
),
∴Tn=b1+b2+…+bn=
[(
-
)+(
-
)+…+(
-
)]=
(
-
)
当n→+∞时,
→0,Tn→
,
∴Tn≤
,又Tn≤M对一切正整数n都成立,
∴Mmin=
.
∴2Sn-1=nan-1+n-2,n≥2,②
①-②,得:2an=(n+1)an-nan-1+1,n≥2.
∴(n-1)an-nan-1=-1,
∴
| an |
| n |
| an-1 |
| n-1 |
| 1 |
| n(n-1) |
| 1 |
| n |
| 1 |
| n-1 |
∴(
| an |
| n |
| an-1 |
| n-1 |
| an-1 |
| n-1 |
| an-2 |
| n-2 |
| a2 |
| 2 |
| a1 |
| 1 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n-1 |
| 1 |
| n-2 |
| 1 |
| 2 |
即
| an |
| n |
| a1 |
| 1 |
| 1 |
| n |
∴
| an |
| n |
| 1 |
| n |
∴an=2n+1.
(2)∵bn=
| 1 |
| anan+1 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴Tn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
当n→+∞时,
| 1 |
| 2n+3 |
| 1 |
| 6 |
∴Tn≤
| 1 |
| 6 |
∴Mmin=
| 1 |
| 6 |
点评:本题考查数列递推关系的应用,考查累加法与错位相减法求和,(1)中(n-1)an-nan-1=-1⇒
-
=
-
(n≥2)是关键,考查转化思想,是难题.
| an |
| n |
| an-1 |
| n-1 |
| 1 |
| n |
| 1 |
| n-1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,已知向量
=(1,-2),
-
=(2,-3),
=(x,9),若(2
+
)∥
,则x=( )
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| A、-2 | B、-4 | C、-3 | D、-1 |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、±
| ||||
D、y=±
|
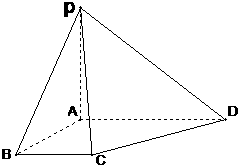 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2 正方体ABCD-A1B1C1D1的棱长为2,O是AC与BD的交点,E是B1B上一点,且B1E=
正方体ABCD-A1B1C1D1的棱长为2,O是AC与BD的交点,E是B1B上一点,且B1E=