题目内容
11.若幂函数f(x)的图象经过(-$\sqrt{2}$,2),则f(4)=16.分析 设幂函数f(x)=xα,把点(-$\sqrt{2}$,2)代入解析式求出α,即可求出函数的解析式和f(4)的值.
解答 解:设幂函数f(x)=xα,
∵函数f(x)的图象经过(-$\sqrt{2}$,2),
∴(-$\sqrt{2}$)α=2,解得α=2,
则f(x)=x2,∴f(4)=16,
故答案为:16.
点评 本题考查幂函数的解析式的求法:待定系数法,属于基础题.

练习册系列答案
相关题目
19.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则( )
| A. | 直线a必垂直于平面β | B. | 直线b必垂直于平面α | ||
| C. | 直线a不一定垂直于平面β | D. | 过a的平面与过b的平面垂直 |
6.设集合A={x|y=lg(x-1)},集合B={y|y=-x2+2},则A∩B等于( )
| A. | (1,2) | B. | (1,2] | C. | [1,2) | D. | [1,2] |
3.已知直线m,n和平面α,下列推理正确的是( )
| A. | $\left.{\begin{array}{l}{m⊥n}\\{n?α}\end{array}}\right\}⇒m⊥α$ | B. | $\left.{\begin{array}{l}{m⊥n}\\{n⊥α}\end{array}}\right\}⇒m∥α$ | C. | $\left.{\begin{array}{l}{m⊥α}\\{n∥α}\end{array}}\right\}⇒m⊥n$ | D. | $\left.{\begin{array}{l}{m∥α}\\{n?α}\end{array}}\right\}⇒m∥n$ |
20.为了得到函数y=sin3x-$\sqrt{3}$cos3x的图象( )
| A. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| B. | 只要将函数y=sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| C. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{9}$个单位 | |
| D. | 只要将函数y=sin3x的图象向右平移$\frac{π}{9}$个单位 |
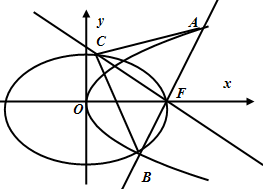 如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.
如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.