题目内容
一个几何体的三视图如图所示，则该几何体的体积为 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图得出该几何体是下部正方体，上部是四棱锥的组合体，求出它的体积即可．
解答：
解：根据几何体的三视图知，
该几何体是下部是楞长为4的正方体，上部是高为3的四棱锥的组合体，
∴该几何体的体积是
V组合体=V正方体+V四棱锥=43+
×42×3=80．
故答案为：80．
该几何体是下部是楞长为4的正方体，上部是高为3的四棱锥的组合体，
∴该几何体的体积是
V组合体=V正方体+V四棱锥=43+
| 1 |
| 3 |
故答案为：80．
点评：本题考查了空间几何体的三视图的应用问题，也考查了求几何体的体积的应用问题，是基础题．
练习册系列答案
53随堂测系列答案
相关题目
已知向量
，
的夹角为120°，|
|=2，且
•
=-8，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| b |
| A、6 | B、7 | C、8 | D、9 |
已知正方体ABCD-A1B1C1D1，过顶点A1作平面α，使得直线AC和BC1平面α所成的角都为30°，这样的平面α可以有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
若a=log23，b=log32，c=esinπ，则a，b，c 的大小关系为（ ）
| A、a＜b＜c |
| B、c＜b＜a |
| C、a＜c＜b |
| D、b＜c＜a |
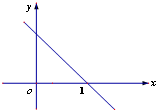函数f（x）的导数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），则f（0）与f（2）的大小关系为（ ）| A、f（0）＜f（2） |
| B、f（0）＞f（2） |
| C、f（0）=f（2） |
| D、无法确定 |