题目内容
当a>e2时,f(x)=|ln|x-1||+ex-a有 个零点.
考点:函数零点的判定定理
专题:函数的性质及应用
分析:把函数f(x)=|ln|x-1||+ex-a的零点转化为两个函数y=|ln|x-1||与y=-ex+a图象交点的横坐标,画图即可得到答案.
解答:
解:由|x-1|>0,得x≠1.
∴f(x)的定义域为{x|x≠1},
由|x-1|≥1,得x≤0或x≥2,
由0<|x-1|<1,得0<x<2.
∴f(x)=|ln|x-1||+ex-a的零点即为方程|ln|x-1||+ex-a=0的根,
也就是方程|ln|x-1||=-ex+a的根,
即函数y=|ln|x-1||与y=-ex+a图象交点的横坐标,
又a>e2,图象如图,
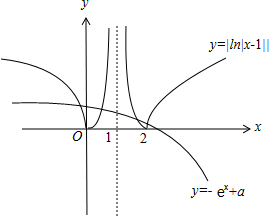
由图可知,f(x)=|ln|x-1||+ex-a有4个零点.
故答案为:4.
∴f(x)的定义域为{x|x≠1},
由|x-1|≥1,得x≤0或x≥2,
由0<|x-1|<1,得0<x<2.
∴f(x)=|ln|x-1||+ex-a的零点即为方程|ln|x-1||+ex-a=0的根,
也就是方程|ln|x-1||=-ex+a的根,
即函数y=|ln|x-1||与y=-ex+a图象交点的横坐标,
又a>e2,图象如图,
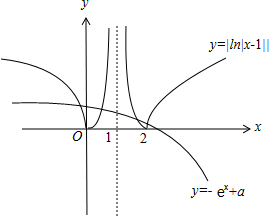
由图可知,f(x)=|ln|x-1||+ex-a有4个零点.
故答案为:4.
点评:本题考查了函数零点的判断,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数f(x)对定义域R内的任意x都有f(2+x)=f(6-x),且当x≠4时其导函数f′(x)满足xf′(x)>4f′(x),若9<a<27,则( )
A、f(2
| ||
B、f(6)<f(2
| ||
C、f(1og3a)<f(2
| ||
D、f(1og3a)<f(6)<f(2
|