题目内容
5.已知tan(x+$\frac{π}{2}$)=5,则$\frac{1}{sinxcosx}$=( )| A. | $\frac{26}{5}$ | B. | -$\frac{26}{5}$ | C. | ±$\frac{26}{5}$ | D. | -$\frac{5}{26}$ |
分析 由已知利用诱导公式求得tanx,把1用sin2x+cos2x代替,然后化弦为切得答案.
解答 解:∵tan(x+$\frac{π}{2}$)=5,∴cotx=-5,则tanx=-$\frac{1}{5}$,
$\frac{1}{sinxcosx}$=$\frac{si{n}^{2}x+co{s}^{2}x}{sinxcosx}=\frac{1+ta{n}^{2}x}{tanx}=\frac{1+\frac{1}{25}}{-\frac{1}{5}}=-\frac{26}{5}$.
故选:B.
点评 本题考查三角函数的化简求值,考查诱导公式及同角三角函数基本关系式的应用,是基础题.

练习册系列答案
相关题目
15.若$tanθ=\frac{1}{2}$,则cos2θ+sin2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
15.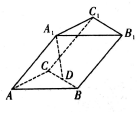 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
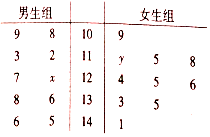 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: