题目内容
函数f（x）=x|x-a|-2（0≤x≤1）的最小值为 ．
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：由0≤x≤1可观察到x|x-a|≥0且0一定能取到，故可直接求最小值．
解答：
解：∵0≤x≤1，且|x-a|≥0；
∴（x|x-a|）min=0（x=0时一定成立）；
∴（x|x-a|-2）min=-2；
即函数f（x）=x|x-a|-2（0≤x≤1）的最小值为-2．
故答案为：-2．
∴（x|x-a|）min=0（x=0时一定成立）；
∴（x|x-a|-2）min=-2；
即函数f（x）=x|x-a|-2（0≤x≤1）的最小值为-2．
故答案为：-2．
点评：本题考查了函数的最值的求法，属于基础题．
练习册系列答案
相关题目
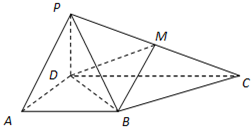如图，四棱锥P-ABCD中，底面ABCD为梯形，∠DAB=60°，AB∥CD，AD=CD=2AB，PD⊥底面ABCD，M为PC的中点．