题目内容
设椭圆
+
=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B.已知|AB|=
|F1F2|.
(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过原点O的直线l与该圆相切,求直线l的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过原点O的直线l与该圆相切,求直线l的斜率.
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(1)由题意设椭圆右焦点F2的坐标为(c,0),结合|AB|=
|F1F2|,可得a2+b2=3c2,再结合隐含条件
b2=a2-c2得到a,c的关系式,则椭圆的离心率可求;
(2)由题意设出椭圆方程为
+
=1.设P(x0,y0).由F1(-c,0),B(0,c),求得
,
的坐标,利用
•
=0得到(x0+c)c+y0c=0,从而得到x0+y0+c=0.再由点P在椭圆上,得到
+
=1.两式联立得到3x20+4cx0=0.根据点P不是椭圆的顶点得到x0=-
c.进一步得到y0=
,
再设圆的圆心为T(x1,y1),则x1=
=-
c,y1=
=
c,求出圆的半径r再由直线l与圆相切列式求得k的值.
| ||
| 2 |
b2=a2-c2得到a,c的关系式,则椭圆的离心率可求;
(2)由题意设出椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
| F1P |
| F1B |
的坐标,利用
| F1P |
| F1B |
| x02 |
| 2c2 |
| y02 |
| c2 |
| 4 |
| 3 |
| c |
| 3 |
再设圆的圆心为T(x1,y1),则x1=
-
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
解答:
解:(1)设椭圆右焦点F2的坐标为(c,0).
由|AB|=
|F1F2|,可得a2+b2=3c2.
又b2=a2-c2,则2a2=4c2,
=
,
∴椭圆的离心率e=
;
(2)由(1)知a2=2c2,b2=c2.故椭圆方程为
+
=1.
设P(x0,y0).由F1(-c,0),B(0,c),
得
=(x0+c,y0),
=(c,c).
由已知,有
•
=0,即(x0+c)c+y0c=0.
又c≠0,故有x0+y0+c=0.①
又∵点P在椭圆上,
∴
+
=1.②
由①和②可得3x20+4cx0=0.
而点P不是椭圆的顶点,故x0=-
c.代入①得y0=
,
即点P的坐标为(-
,
).
设圆的圆心为T(x1,y1),则x1=
=-
c,y1=
=
c,
进而圆的半径r=
=
=
c.
设直线l的斜率为k,依题意,直线l的方程为y=kx.
由l与圆相切,可得
=r,即
=
c,整理得k2-8k+1=0,解得k=4±
,
∴直线l的斜率为4+
或4-
.
由|AB|=
| ||
| 2 |
又b2=a2-c2,则2a2=4c2,
| c2 |
| a2 |
| 1 |
| 2 |
∴椭圆的离心率e=
| ||
| 2 |
(2)由(1)知a2=2c2,b2=c2.故椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
设P(x0,y0).由F1(-c,0),B(0,c),
得
| F1P |
| F1B |
由已知,有
| F1P |
| F1B |
又c≠0,故有x0+y0+c=0.①
又∵点P在椭圆上,
∴
| x02 |
| 2c2 |
| y02 |
| c2 |
由①和②可得3x20+4cx0=0.
而点P不是椭圆的顶点,故x0=-
| 4 |
| 3 |
| c |
| 3 |
即点P的坐标为(-
| 4c |
| 3 |
| c |
| 3 |
设圆的圆心为T(x1,y1),则x1=
-
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
进而圆的半径r=
| (x1-0)2+(y1-c)2 |
(-
|
| ||
| 3 |
设直线l的斜率为k,依题意,直线l的方程为y=kx.
由l与圆相切,可得
| |kx1-y1| | ||
|
|k(-
| ||||
|
| ||
| 3 |
| 15 |
∴直线l的斜率为4+
| 15 |
| 15 |
点评:本题主要考查了直线与圆锥曲线的位置关系的应用,考查了向量在解题中的应用,圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理能力和逻辑思维能力,是压轴题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
给出下列命题:
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
(x-2)≥0的解集为[2,+∞);
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
| x-1 |
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
| A、①④ | B、④⑤ | C、③⑤ | D、②③ |
已知α为第三象限角,且sinα(sinα+cosα)=cos2α,则tan2α的值为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、 |
C、 |
D、 |
方程x3-6x2+9x-10=0的实根个数是( )
| A、3 | B、2 | C、1 | D、0 |
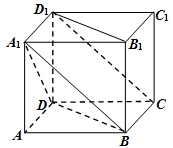 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60° 如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.