题目内容
若函数f（x）为定义在R上的奇函数，且在（0，+∞）上是增函数，又f（2）=0，则不等式
＜0的解集为 ．
| f(x)-f(-2) |
| x |
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据已知条件知f（x）在（-∞，0）上是增函数，f（-2）=0，所以原不等式可变成
，或
，根据f（x）的单调性解这两个不等式组即得原不等式的解集．
|
|
解答：
解：原不等式变成：
（Ⅰ），或
（Ⅱ），∵f（x）是奇函数，在（0，+∞）上是增函数，∴在（-∞，0）上也是增函数；
又f（2）=0，∴f（-2）=f（2）=0；
∴解不等式组（Ⅰ）得-2＜x＜0，解不等式组（Ⅱ）变成
，解得0＜x＜2；
∴原不等式的解集是（-2，0）∪（0，2）．
故答案为：（-2，0）∪（0，2）．
|
|
又f（2）=0，∴f（-2）=f（2）=0；
∴解不等式组（Ⅰ）得-2＜x＜0，解不等式组（Ⅱ）变成
|
∴原不等式的解集是（-2，0）∪（0，2）．
故答案为：（-2，0）∪（0，2）．
点评：考查奇函数的定义，奇函数在对称区间上的单调性特点，以及解分式不等式．
练习册系列答案
相关题目
设x、y满足约束条件
，则z=3x+2y的最大值时（ ）
|
| A、3 | B、4 | C、5 | D、6 |
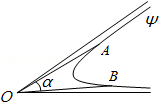如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：f（x）=
|
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列命题：
①y=1是幂函数；
②函数f（x）=2x-log2x的零点有1个；
③
（x-2）≥0的解集为[2，+∞）；
④“x＜1”是“x＜2”的充分不必要条件；
⑤函数y=x3在点O（0，0）处切线是x轴；
其中真命题的序号是（ ）
①y=1是幂函数；
②函数f（x）=2x-log2x的零点有1个；
③
| x-1 |
④“x＜1”是“x＜2”的充分不必要条件；
⑤函数y=x3在点O（0，0）处切线是x轴；
其中真命题的序号是（ ）
| A、①④ | B、④⑤ | C、③⑤ | D、②③ |
下列函数中是偶函数且在（0，+∞）上单调递增的是（ ）
| A、y=2-x |
| B、y=lnx |
| C、y=x-2 |
| D、y=|x|-1 |
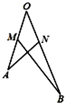如图，M、N分别是线段OA、OB上的点，OM=MA=ON=1，NB=2，设