题目内容
类比“两角和与差的正弦公式”的形式，对于给定的两个函数：S（x）=
，C（x）=
，下面正确的运算公式是（ ）
①S（x+y）=S（x）C（y）+C（x）S（y）
②S（x-y）=S（x）C（y）-C（x）S（y）
③2S（x+y）=S（x）C（y）+C（x）S（y）
④2S（x-y）=S（x）C（y）-C（x）S（y）
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
①S（x+y）=S（x）C（y）+C（x）S（y）
②S（x-y）=S（x）C（y）-C（x）S（y）
③2S（x+y）=S（x）C（y）+C（x）S（y）
④2S（x-y）=S（x）C（y）-C（x）S（y）
| A、①② | B、③④ | C、①④ | D、②③ |
考点：导数的运算
专题：推理和证明
分析：写出“两角和与差的正余弦公式”的形式，写出类比结论．
解答：
解S（x）=
，C（x）=
，
∵“两角和与差的正余弦公式”的形式是
sin（x+y）=sinxcosy+cosxsiny
sin（x-y）=sinxcosy-cosxsiny
cos（x+y）=cosxcosy-sinxsiny
cos（x-y）=cosxcosy+sinxsiny
对于S（x）=
，C（x）=
，
对于①S（x+y）=S（x）C（y）+C（x）S（y）
②S（x-y）=S（x）C（y）-C（x）S（y）
③2S（x+y）=S（x）C（y）+C（x）S（y）
④2S（x-y）=S（x）C（y）-C（x）S（y）
于是类比可以得到答案，
对于S（x+y）=
，
S（x）C（y）+C（x）S（y）=
•
+
•
=
（ex+y-e-x-y）
故①正确，③错误，
同理可到②正确，④错误，
故①②正确．
故选：A
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
∵“两角和与差的正余弦公式”的形式是
sin（x+y）=sinxcosy+cosxsiny
sin（x-y）=sinxcosy-cosxsiny
cos（x+y）=cosxcosy-sinxsiny
cos（x-y）=cosxcosy+sinxsiny
对于S（x）=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
对于①S（x+y）=S（x）C（y）+C（x）S（y）
②S（x-y）=S（x）C（y）-C（x）S（y）
③2S（x+y）=S（x）C（y）+C（x）S（y）
④2S（x-y）=S（x）C（y）-C（x）S（y）
于是类比可以得到答案，
对于S（x+y）=
| ex+y-e-x-y |
| 2 |
S（x）C（y）+C（x）S（y）=
| ex-e-x |
| 2 |
| ey+e-y |
| 2 |
| ey-e-y |
| 2 |
| ex+e-x |
| 2 |
| 1 |
| 2 |
故①正确，③错误，
同理可到②正确，④错误，
故①②正确．
故选：A
点评：本题考查利用类比推理从形式上写出类比结论．写类比结论时：先找类比对象，再找类比元素．
练习册系列答案
相关题目
若a＞0＞b，则下列不等式中成立的是（ ）
A、
| ||||
B、
| ||||
| C、|a|＞|b| | ||||
| D、a2＞b2 |
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2+2x，则满足f（2-x2）＜f（x）的实数x的取值范围为（ ）
| A、（1，+∞） |
| B、（-∞，-2） |
| C、（-∞，-2）∪（1，+∞） |
| D、（-2，1） |
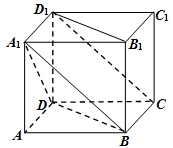如图，在底面为平行四边形的四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，AD=1，CD=2，∠DCB=60°
如图，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC=30°，AF⊥PC于点F，FE∥CD交PD于点E．