题目内容
若点P,Q在抛物线y2=4x上,O是坐标原点,且
•
=0.则直线PQ恒过的顶点的坐标是 .
| OP |
| OQ |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设出A,B的坐标,讨论直线斜率存在时,联立直线方程与抛物线方程,利用消元法得到关于x的一元二次方程,由
•
=0.得x1x2+y1y2=0,建立关于参数k,b的关系,消去b可得直线恒过(4,0).
| OP |
| OQ |
解答:
解:设点A,B的坐标分别为(x1,y1),(x2,y2)
当直线l存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.
联立方程得:
,消去y得k2x2+(2kb-4)x+b2=0
则x1x2=
,
由y12=4x1,y22=4x2,
则y1y2=4•
,
又
•
=0,则x1x2+y1y2=0,
即
+
=0,
解得b=0(舍去)或b=-4k,
故直线l的方程为:y=kx-k=k(x-4),故直线过定点(4,0),
故答案为:(4,0).
当直线l存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.
联立方程得:
|
则x1x2=
| b2 |
| k2 |
由y12=4x1,y22=4x2,
则y1y2=4•
| b |
| k |
又
| OP |
| OQ |
即
| b2 |
| k2 |
| 4b |
| k |
解得b=0(舍去)或b=-4k,
故直线l的方程为:y=kx-k=k(x-4),故直线过定点(4,0),
故答案为:(4,0).
点评:本题考查向量垂直的条件,同时考查直线与抛物线的位置关系,以及证明直线恒过定点,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
将cos(π+2)化为某个锐角的三角函数为( )
| A、cos2 |
| B、-cos2 |
| C、-cos(π-2) |
| D、cos(π-2) |
函数f(x)=x
-(
)x的零点所在的一个区间为( )
| 1 |
| 2 |
| 1 |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(1,2) |
曲线
+
=1与曲线
+
=1(0<k<9)具有( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、相等的长、短轴 |
| B、相等的焦距 |
| C、相等的离心率 |
| D、相同的准线 |
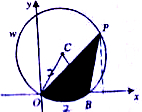 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).