题目内容
动点到直线x=6的距离是它到点A(1,0)的距离的2倍,那么动点的轨迹方程是 .
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用动点到直线x=6的距离是它到点A(1,0)的距离的2倍,建立方程,化简即可求出动点的轨迹方程.
解答:
解:由题意,|x-6|=2
,
化简可得3x2+4y2+4x-32=0.
故答案为:3x2+4y2+4x-32=0.
| (x-1)2+y2 |
化简可得3x2+4y2+4x-32=0.
故答案为:3x2+4y2+4x-32=0.
点评:本题考查轨迹方程,考查学生的计算能力,比较基础.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知数列{an}的首项a1=1,an+1=
+1,则这个数列的第四项是( )
| 2 |
| an |
A、
| ||
B、
| ||
C、
| ||
| D、6 |
若
sinα+sin(
-α)=
,则sin(
+2α)的值为( )
| 3 |
| 3π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的体积是( )
A、20
| ||||
B、
| ||||
C、
| ||||
| D、50π |
如果命题“p∧q”是假命题,“非q”也是假命题,则( )
| A、命题“非p∨q”是假命题 |
| B、命题“p∨q”是假命题 |
| C、命题“非p∧q”是真命题 |
| D、命题“p∧非q”是真命题 |
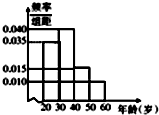 某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.
某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.