题目内容
函数f(x)=x
-(
)x的零点所在的一个区间为( )
| 1 |
| 2 |
| 1 |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(1,2) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:直接利用函数的零点判定定理,判断即可.
解答:
解:由函数的零点判定定理可知,连续函数f(x)在(a,b)时有零点,必有f(a)f(b)<0.
f(0)=-1<0.
f(
)=(
)
-(
)
=
-(
)
<0.
f(
)=(
)
-(
)
=0.
f(1)=1-(
)1>0.
f(2)=(2)
-(
)2>0.
所以函数的零点是x=
.
故选:B.
f(0)=-1<0.
f(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(1)=1-(
| 1 |
| 2 |
f(2)=(2)
| 1 |
| 2 |
| 1 |
| 2 |
所以函数的零点是x=
| 1 |
| 2 |
故选:B.
点评:本题考查函数点了点判定定理的应用,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)为偶函数,当x≥0时,f(x)=
,则不等式f(x)≤
的解集为( )
|
| 1 |
| 2 |
A、[
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[-
|
定义区间[x1,x2]长度为x2-x1,(x2>x1),已知函数f(x)=
(a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值为( )
| (a2+a)x-1 |
| a2x |
A、
| ||||
| B、a>1或a<-3 | ||||
| C、a>1 | ||||
| D、3 |
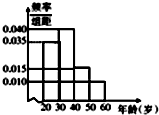 某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.
某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.