题目内容

已知⊙C的方程为x2+（y-1）2=5，直线l经过点（1，1）．
（1）若直线l的倾斜角为
π
4
，求直线l的方程；
（2）设直线l与⊙C交于A、B两点，若|AB|=
17
，求直线l的斜率．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）求出直线的斜率，即可求直线l的方程；
（2）去出弦心距、利用点到直线的距离公式可得直线的斜率．
解答： 解：（1）∵直线l的倾斜角为
π
4
，
∴直线l的斜率为1，
∵直线l经过点（1，1），
∴直线l的方程为x-y=0；
（2）由于半径r=
5
，|AB|=
17
，∴弦心距d=
3
2
，
再由点到直线的距离公式可得d=
|0-1+1-m|
m2+1
=
3
2
，
解得m=±
3
．
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知f（x）为偶函数，当x≥0时，f（x）=
cosπx，x∈[0，
1
2
]
2x-1，x∈(
1
2
，+∞)
，则不等式f（x）≤
1
2
的解集为（　　）
A、[
1
4
，
2
3
]∪[
4
3
，
7
4
]
B、[-
3
4
，-
1
3
]∪[
1
4
，
2
3
]
C、[
1
3
，
3
4
]∪[
4
3
，
7
4
]
D、[-
3
4
，-
1
3
]∪[
1
3
，
3
4
]
若点P，Q在抛物线y2=4x上，O是坐标原点，且
OP
•
OQ
=0．则直线PQ恒过的顶点的坐标是
 
．
已知一次函数f（x）=ax-2．
（1）解关于x的不等式|f（x）|＜4；
（2）若不等式|f（x）|≤3对任意的x∈[0，1]恒成立，求实数a的范围．
已知函数f（x）=a|x+1|-b|2x-4|，当a=1，b=
1
2
时，解不等式f（x）≤0．
已知等差数列{an}的前n项和sn，且s4=16，a4=7．
（1）求数列{an}的通项公式；
（2）设bn=
1
anan+1
，求数列{bn}的前n项和为Tn．
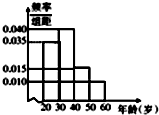某学校有120名教师，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60）分组，其频率分布直方图如右图所示．学校为了适应新课程改革，要求每名教师都要参加甲、乙两项培训，培训结束后进行结业考试，已知各年龄段两项培训结业考试成绩优秀的人数如下表所示．假设两项培训是相互独立的，结业考试也互不影响．
年龄分组甲项培训成绩优秀人数乙项培训成绩优秀人数
[20，30）3018
[30，40）3624
[40，50）129
[50，60）43
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求各年龄段应分别抽取的人数，并估计全校教师的平均年龄；
（2）随机从年龄段[20，30）和[30，40）中各抽取1人，求这两人中至少有一人在甲、乙两项培训结业考试成绩为优秀的概率．
已知数列{an}的首项a1=1，an+1=
2
an
+1，则这个数列的第四项是（　　）
A、
11
7
B、
11
5
C、
21
11
D、6
数列{an}满足a1=1，
1
2an+1
=
1
2an
+1（n∈N*）．
（Ⅰ）求证{
1
an
}是等差数列；
（Ⅱ）若bn=an•an+1，求{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网