题目内容
求该四棱锥的体积．
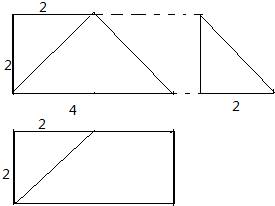
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是一个四棱锥，四棱锥的底面是一个长为4，宽为2的矩形，顶点底面的面积，四棱锥的一个侧面与底面垂直，四棱锥的高是2，即可得到结果．
解答：
解：由三视图知，几何体是一个四棱锥，
∵四棱锥的底面是一个长为4，宽为2的矩形，
∴面积是4×2=8，
∵四棱锥的一个侧面与底面垂直，高为2，
∴体积为
×8×2=
∵四棱锥的底面是一个长为4，宽为2的矩形，
∴面积是4×2=8，
∵四棱锥的一个侧面与底面垂直，高为2，
∴体积为
| 1 |
| 3 |
| 16 |
| 3 |
点评：本题考查由三视图求几何体的表体积，考查由三视图还原几何体，是一个基础题．
练习册系列答案
科学实验活动册系列答案
相关题目
定义区间[x1，x2]长度为x2-x1，（x2＞x1），已知函数f（x）=
（a∈R，a≠0）的定义域与值域都是[m，n]，则区间[m，n]取最大长度时a的值为（ ）
| (a2+a)x-1 |
| a2x |
A、
| ||||
| B、a＞1或a＜-3 | ||||
| C、a＞1 | ||||
| D、3 |
三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC外接球的体积是（ ）
A、20
| ||||
B、
| ||||
C、
| ||||
| D、50π |