题目内容
曲线
+
=1与曲线
+
=1（0＜k＜9）具有（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、相等的长、短轴 |
| B、相等的焦距 |
| C、相等的离心率 |
| D、相同的准线 |
考点：双曲线的简单性质,椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出椭圆
+
=1的a1=5，b1=3，c1=4，以及离心率和准线，判断曲线
+
=1（0＜k＜9）为椭圆，求出a2，b2，c2，和离心率、准线方程，即可得到结论．
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
解答：
解：椭圆
+
=1的a1=5，b1=3，c1=
=4，
e1=
=
，准线方程为x=±
，
曲线
+
=1（0＜k＜9）为椭圆，
且a2=
，b2=
，c2=
=4，
e2=
=
，准线方程为x=±
，
则两曲线的长、短轴不相等，选项A错误；它们的焦距均为8，则选项B正确；
它们的离心率显然不等，则选项C错误；它们的准线不相同，则D错误．
故选B．
| x2 |
| 25 |
| y2 |
| 9 |
| 25-9 |
e1=
| c1 |
| a1 |
| 4 |
| 5 |
| 25 |
| 4 |
曲线
| x2 |
| 25-k |
| y2 |
| 9-k |
且a2=
| 25-k |
| 9-k |
| 25-k-(9-k) |
e2=
| c2 |
| a2 |
| 4 | ||
|
| 25-k |
| 4 |
则两曲线的长、短轴不相等，选项A错误；它们的焦距均为8，则选项B正确；
它们的离心率显然不等，则选项C错误；它们的准线不相同，则D错误．
故选B．
点评：本题考查椭圆的方程和性质，分别求出它们的a，b，c是解题的关键，属于基础题和易错题．
练习册系列答案
相关题目
已知圆锥的母线长为5cm，圆锥的侧面展开图如图所示，且∠AOA1=120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．则蚂蚁爬行的最短路程长为（ ）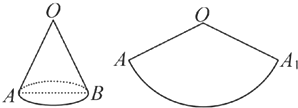 
| A、8 cm | ||
B、5
| ||
| C、10 cm | ||
| D、5πcm |
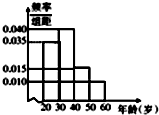某学校有120名教师，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60）分组，其频率分布直方图如右图所示．学校为了适应新课程改革，要求每名教师都要参加甲、乙两项培训，培训结束后进行结业考试，已知各年龄段两项培训结业考试成绩优秀的人数如下表所示．假设两项培训是相互独立的，结业考试也互不影响．