题目内容
f(x)是定义在R上的偶函数,满足f(x+2)+f(x)=2,当2≤x<3时,f(x)=x,则f(5.5)等于( )
| A、-0.5 | B、1.5 |
| C、2.5 | D、5.5 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,根据f(x+2)+f(x)=2,得到f(x+2)=2-f(x),然后,结合该关系式,进行求解即可.
解答:
解:∵f(x+2)+f(x)=2,
∴f(x+2)=2-f(x),
∵f(5.5)=f(3.5+2)
∴f(5.5)=2-f(3.5)
f(3.5)=f(1.5+2)=2-f(1.5)
f(1.5)=f(-0.5+2)=2-f(-0.5)
f(-0.5)=f(-2.5+2)=2-f(-2.5)
∵f(x)是定义在R上的偶函数,
∴f(-2.5)=f(2.5)=2.5,
∴f(5.5)=2.5
故选:C
∴f(x+2)=2-f(x),
∵f(5.5)=f(3.5+2)
∴f(5.5)=2-f(3.5)
f(3.5)=f(1.5+2)=2-f(1.5)
f(1.5)=f(-0.5+2)=2-f(-0.5)
f(-0.5)=f(-2.5+2)=2-f(-2.5)
∵f(x)是定义在R上的偶函数,
∴f(-2.5)=f(2.5)=2.5,
∴f(5.5)=2.5
故选:C
点评:本题重点考查了函数的基本性质、函数的偶函数的重要性质等知识,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某产品生产厂家的市场部在对4家商场进行调研时,获得该产品售价x(单位:元)和销售量y(单位:件)之间的四组数据如表:
为决策产品的市场指导价,用最小二乘法求得销售量y与售价x之间的线性回归方程y=-1.4x+a,那么方程中的a值为( )
| 售价x | 4 | 4.5 | 5.5 | 6 |
| 销售量y | 12 | 11 | 10 | 9 |
| A、17 | B、17.5 |
| C、18 | D、18.5 |
变量 x y、满足线性约束条件
,则目标函数 z=kx-y,仅在点(0,2)取得最小值,则k的取值范围是( )
|
| A、k<-3 |
| B、k>1? |
| C、-3<k<1 |
| D、-1<k<1 |
若集合A={x|x>1},B={x|2x<8},则A∩B=( )
| A、{x|x≤3} |
| B、{x|x>1} |
| C、{x|1<x<3} |
| D、{x|1<x<2} |
已知程序框图如图所示,输入x的值为7时,输出y的值为( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是( )
| A、πR2 |
| B、2πR2 |
| C、3πR2 |
| D、4πR2 |
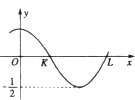 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(| 1 |
| 6 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|