题目内容
10.设已知抛物线C:y2=2px的焦点为F1,过F1的直线l与曲线C相交于M,N两点.(1)若直线l的倾斜角为60°,且|MN|=$\frac{16}{3}$,求p;
(2)若p=2,椭圆$\frac{{x}^{2}}{2}$+y2=1上两个点P,Q,满足:P,Q,F1三点共线且PQ⊥MN,求四边形PMQN的面积的最小值.
分析 (1)直线l的方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),代入抛物线方程,利用弦长公式,求p;
(2)分类讨论,求出弦长,表示面积,即可得出结论.
解答 解:(1)直线l的方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),代入抛物线方程,整理可得$3{x}^{2}-5px+\frac{3{p}^{2}}{4}$=0,
∴xN+xM=$\frac{5p}{3}$,
∵|MN|=$\frac{16}{3}$,
∴$\frac{5p}{3}$+p=$\frac{16}{3}$,∴p=2;
(2)当直线MN斜率不存在时,直线PQ斜率为0,此时|MN|=4,|PQ|=2$\sqrt{2}$,SPMQN=4$\sqrt{2}$.
当直线MN斜率存在时,设方程为y=k(x-1)(k≠0),代入抛物线可得k2x2-(2k2+4)x+k2=0,
∴xM+xN=$\frac{4}{{k}^{2}}$+2,
∴|MN|=$\frac{4}{{k}^{2}}$+4
由PQ⊥MN,可设PQ的方程y=-$\frac{1}{k}$(x-1),代入椭圆方程得(k2+2)x2-4x+2-2k2=0,
∴xP+xQ=$\frac{4}{2+{k}^{2}}$,xPxQ=$\frac{2-2{k}^{2}}{2+{k}^{2}}$,
∴PQ|=$\sqrt{1+\frac{1}{{k}^{2}}}$•$\sqrt{(\frac{4}{2+{k}^{2}})^{2}-4•\frac{2-2{k}^{2}}{2+{k}^{2}}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{2+{k}^{2}}$,
∴S=$\frac{4\sqrt{2}(1+{k}^{2})^{2}}{{k}^{2}(2+{k}^{2})}$,
令t=1+k2(t>1),S=$\frac{4\sqrt{2}{t}^{2}}{{t}^{2}-1}$=4$\sqrt{2}$(1+$\frac{1}{{t}^{2}-1}$)>4$\sqrt{2}$,
∴四边形PMQN的面积的最小值为4$\sqrt{2}$.
点评 本题考查抛物线的方程与性质,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| A. | ∅ | B. | {1} | C. | {-2,0,1} | D. | {-1,0,1,2} |
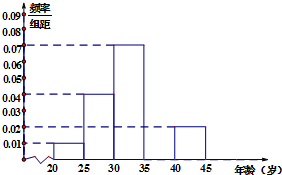 当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:| 组数 | 分组(单位:岁) | 频数 | 频率 |
| 1 | [20,25) | 5 | 0.05 |
| 2 | [25,30) | 20 | 0.20 |
| 3 | [30,35) | a | 0.35 |
| 4 | [35,40) | 30 | b |
| 5 | [40,45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查,再从这6名市民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率?
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{3}$ | a | b |
| A. | $\frac{5}{6}$ | B. | $\frac{41}{48}$ | C. | 1 | D. | $\frac{2}{3}$ |
| A. | [-1,3] | B. | (-1,3) | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1)∪(3,+∞) |
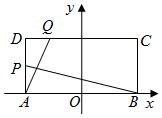 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.