题目内容
20.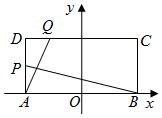 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.(Ⅰ)求椭圆E的方程;
(Ⅱ)设R为椭圆E的右顶点,M为椭圆E第一象限部分上一点,作MN垂直于y轴,垂足为N,求梯形ORMN面积的最大值.
分析 (Ⅰ)由题可知,$\frac{y_1}{2}=\frac{{{x_1}+2}}{4},\frac{y}{x+2}=\frac{2}{{{x_1}+2}},\frac{y}{x-2}=\frac{y_1}{-4}$,整理即可求得椭圆E的方程;
(Ⅱ)由${y_0}=\frac{1}{2}\sqrt{4-x_0^2}$,则梯形面积$S=\frac{1}{2}(2+{x_0}){y_0}$=$\frac{1}{4}\sqrt{(4-x_0^2){{(2+{x_0})}^2}}$,t=2+x0,2<t<4,$S=\frac{1}{4}\sqrt{4{t^3}-{t^4}}$,根据函数的单调性即可求得梯形ORMN面积的最大值.
解答 解:(Ⅰ)设AQ于BP交点C为(x,y),P(-2,y1),Q(x1,2),
由题可知,$\frac{y_1}{2}=\frac{{{x_1}+2}}{4},\frac{y}{x+2}=\frac{2}{{{x_1}+2}},\frac{y}{x-2}=\frac{y_1}{-4}$,(4分)
从而有$\frac{-4y}{x-2}=\frac{x+2}{y}$,整理得$\frac{x^2}{4}+{y^2}=1$,即为椭圆方程,
椭圆E的方程$\frac{x^2}{4}+{y^2}=1$;(6分)
(Ⅱ)R(2,0),设M(x0,y0),有${y_0}=\frac{1}{2}\sqrt{4-x_0^2}$,
从而所求梯形面积$S=\frac{1}{2}(2+{x_0}){y_0}$=$\frac{1}{4}\sqrt{(4-x_0^2){{(2+{x_0})}^2}}$,(8分)
令t=2+x0,2<t<4,$S=\frac{1}{4}\sqrt{4{t^3}-{t^4}}$,
令u=4t3-t4,u'=12t2-4t3=4t2(3-t),(10分)
当t∈(2,3)时,u=4t3-t4单调递增,
当t∈(3,4)时,u=4t3-t4单调递减,则当t=3时S取最大值$\frac{{3\sqrt{3}}}{4}$,
梯形ORMN面积的最大值$\frac{{3\sqrt{3}}}{4}$.(12分)
点评 本小题考查椭圆的标准方程及面积最值问题,考查函数单调性与椭圆的综合应用,考查学生的逻辑思维能力和运算求解能力,属于中档题.

| A. | 2 | B. | 2$\sqrt{2}$-1 | C. | 5 | D. | $\sqrt{3}$-1 |
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
| A. | 0 | B. | i | C. | 2i | D. | -i |
| A. | 60 | B. | -60 | C. | 80 | D. | -80 |
