题目内容
1.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{\sqrt{3}x-y≤0}\\{x-\sqrt{3}y+2≥0}\\{y≥0}\end{array}\right.$表示的平面区域的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 由约束条件作出可行域,联立方程组求得三角形三个顶点的坐标,代入三角形面积公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{\sqrt{3}x-y≤0}\\{x-\sqrt{3}y+2≥0}\\{y≥0}\end{array}\right.$作出可行域如图,
不等式组表示的平面区域是一个三角形内部(包括边界).
其中三个顶点的坐标分别为A(-2,0),B(1,$\sqrt{3}$),O(0,0),
∴${S}_{△AOB}=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.已知实数a,b满足(a+2i)•bi=3i+6(i为虚数单位)则在复平面内,复数z=a+bi所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.若数列{an}为等差数列,S99=198,则a48+a49+a50+a51+a52=( )
| A. | 7 | B. | 8 | C. | 10 | D. | 11 |
11.平行四边形ABCD中,AB=2,AD=1,$\overrightarrow{AB}$•$\overrightarrow{AD}$=-1,点M在边CD上,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最大值为( )
| A. | 2 | B. | 2$\sqrt{2}$-1 | C. | 5 | D. | $\sqrt{3}$-1 |
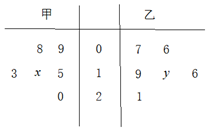 如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.
如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.