题目内容
2.已知随机变量ξ的分布列为下表所示,若$Eξ=\frac{1}{4}$,则Dξ=( )| ξ | -1 | 0 | 1 |
| P | $\frac{1}{3}$ | a | b |
| A. | $\frac{5}{6}$ | B. | $\frac{41}{48}$ | C. | 1 | D. | $\frac{2}{3}$ |
分析 由ξ的分布列的性质得到$\frac{1}{3}$+a+b=1,E(ξ)=$\frac{1}{4}$求得a、b的值,
再利用离散型随机变量方差公式求得D(ξ)的值.
解答 解:由E(ξ)=-1×$\frac{1}{3}$+0×a+1×b=$\frac{1}{4}$,整理得b=$\frac{7}{12}$,
由$\frac{1}{3}$+a+b=1,a=1-$\frac{1}{3}$-$\frac{7}{12}$=$\frac{1}{12}$,
∴D(ξ)=(-1-$\frac{1}{4}$)2×$\frac{1}{3}$+(0-$\frac{1}{4}$)2×$\frac{1}{12}$+(1-$\frac{1}{4}$)2×$\frac{7}{12}$=$\frac{41}{48}$.
故选:B.
点评 本题考查了离散型随机变量的分布列、数学期望和方差的计算问题,是基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.若数列{an}为等差数列,S99=198,则a48+a49+a50+a51+a52=( )
| A. | 7 | B. | 8 | C. | 10 | D. | 11 |
7.设集合M={x|x=2k+1,k∈Z},N={x|x=k+2,k∈Z},则( )
| A. | M?N | B. | M=N | C. | N?M | D. | M∩N=∅ |
11.平行四边形ABCD中,AB=2,AD=1,$\overrightarrow{AB}$•$\overrightarrow{AD}$=-1,点M在边CD上,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最大值为( )
| A. | 2 | B. | 2$\sqrt{2}$-1 | C. | 5 | D. | $\sqrt{3}$-1 |
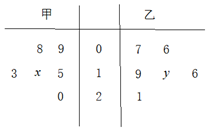 如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.
如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.