题目内容
已知幂函数y=f(x)的图象经过点(8,
),则f(
)的值为( )
| 1 |
| 2 |
| 1 |
| 64 |
| A、3 | ||
B、
| ||
| C、4 | ||
D、
|
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:设出幂函数的解析式,利用已知条件求出解析式,然后求解函数值即可.
解答:
解:设幂函数为y=xα,
∵幂函数y=f(x)的图象经过点(8,
),
∴
=8α,
解得α=-
,幂函数为f(x)=x-
,
则f(
)=(
)-
=4.
故选:C.
∵幂函数y=f(x)的图象经过点(8,
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得α=-
| 1 |
| 3 |
| 1 |
| 3 |
则f(
| 1 |
| 64 |
| 1 |
| 64 |
| 1 |
| 3 |
故选:C.
点评:本题考查幂函数的应用,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a>b,则下列不等式成立的是( )
A、
| ||||
| B、log2a>log2b | ||||
C、
| ||||
| D、2a>2b |
已知椭圆
+
=1的左、右焦点分别为F1,F2,P为椭圆上一点,当|PF1|=λ|PF2|时λ的取值范围( )
| x2 |
| 9 |
| y2 |
| 8 |
| A、[1,3] | ||
| B、[1,2] | ||
C、[
| ||
D、[
|
已知空间四边形ABCD中,棱AB,AC,AD两两互相垂直AB=AC=2,AD=
,则成60°的二面角是( )
| 6 |
| A、B-AD-C |
| B、D-BC-A |
| C、C-BD-A |
| D、B-CD-A |
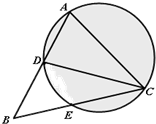 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.