题目内容
设等比数列{an}的前n项的和为Sn,且对任意正整数n,都有a2a8=2a3a6,S5=-62,则a1= .
考点:等比数列的性质
专题:等差数列与等比数列
分析:由等比数列的性质和已知可得公比q,代入求和公式可得a1
解答:
解:由等比数列的性质可得a2a8=a52,a3a6=a4a5,
∵a2a8=2a3a6,∴a52=2a4a5,解得a5=2a4,
∴
=2,即等比数列{an}的公比q=2,
∵S5=
=31a1=-62,∴a1=-2
故答案为:-2
∵a2a8=2a3a6,∴a52=2a4a5,解得a5=2a4,
∴
| a5 |
| a4 |
∵S5=
| a1(1-25) |
| 1-2 |
故答案为:-2
点评:本题考查等比数列的性质,求出公比是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知集合P={x|0≤x≤4},集合N={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
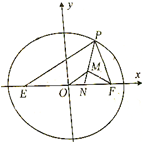 如图,E、F是椭圆G:
如图,E、F是椭圆G:| x2 |
| 4 |
| y2 |
| 3 |
| A、(0,1] | ||||
| B、[-1,1] | ||||
C、[0,
| ||||
| D、[0,1) |
 如图,点P为⊙O的弦AB上的一点,连接OP,过点P作PC⊥OP,PC为⊙O于点C,若OC=4,∠POC=60°,则PA•PB=
如图,点P为⊙O的弦AB上的一点,连接OP,过点P作PC⊥OP,PC为⊙O于点C,若OC=4,∠POC=60°,则PA•PB=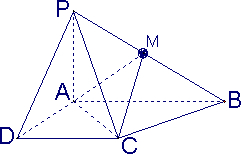 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=