Question

设函数f（x）=

1-|x-1|，x∈(-∞，2) 1 2 f(x-2)，x∈[2，+∞)

，则函数xf（x）-1零点的个数为

 

．

Answer 1

考点：函数与方程的综合运用

专题：函数的性质及应用

分析：由F（x）=0得f（x）=

1

x

，然后分别作出函数f（x）与y=

1

x

的图象，利用数形结合即可得到函数零点的个数．

解答： 解：xf（x）-1=0，可得f（x）-

1

x

=0，
F（x）=f（x）-

1

x

=0得f（x）=

1

x

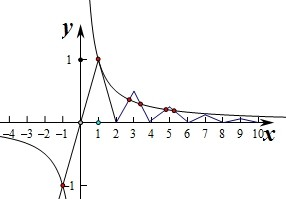
，然后分别作出函数f（x）与y=g（x）=

1

x

的图象如图：
∵当x≥2时，f（x）=

1

2

f（x-2），
∴f（1）=1，g（1）=1，
f（1）=1，g（1）=1，
f（3）=

1

2

f（1）=

1

2

，g（3）=

1

3

，
f（5）=

1

2

f（3）=

1

4

，g（5）=

1

5

，
f（7）=

1

2

f（5）=

1

8

，g（7）=

1

7

，
∴当x＞7时，f（x）＜

1

x

，
由图象可知两个图象的交点个数为6个．
故答案为：6．

点评：本题主要考查方程和函数之间的关系，根据函数零点个数的判断，转化为两个函数图象的交点问题是解决本题的关键，利用数形结合是解决本题的基本思想．本题难度较大，综合性较强．