Question

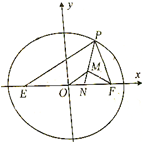如图，E、F是椭圆G：

x2

4

+

y2

3

=1的左、右焦点，P为椭圆上一动点，在△PEF中∠EPF的平分线PN交x轴于点N，作FM⊥PN，垂足为M，则|OM|的取值范围是（　　）

• A、（0，1]
• B、[-1，1]
• C、[0，

  6

  6

  ]
• D、[0，1）

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据椭圆的性质，可得：当P点为椭圆的上（下）顶点时，|OM|取最小值0，当P点无限靠近椭圆的左（右）顶点时，|OM|值无限接近c，进而得到答案．

解答： 解：根据椭圆的性质，可得：当P点为椭圆的上（下）顶点时，
∠EPF的平分线PN交x轴于点N，此时N即为原点O，
作FM⊥PN，垂足为M，此时M即为原点O，
则|OM|取最小值0，
当P点无限靠近椭圆的左（右）顶点时，
∠EPF的平分线PN交x轴于点N，此时N无限靠近椭圆的焦点F（E），
作FM⊥PN，垂足为M，此时M即为椭圆的焦点F（E），
则|OM|＜c=

4-3

=1，
故|OM|的取值范围是[0，1），
故选：D

点评：本题考查的知识点是椭圆的简单性质，其中分析出|OM|的取值范围的上下边界取值时P点的位置，是解答的关键．