题目内容
7.正六边形ABCDEF的对角线AC和CE分别被内点M和N分割,且有$\frac{AM}{AC}=\frac{CN}{CE}=r$.如果B、M、N共线,则r的值为$\frac{{\sqrt{3}}}{3}$.分析 根据正六边形的特点建立坐标系,不妨设边AB=1,求出A、B、C、E的坐标,设M的坐标,由条件和向量相等列出方程,求出M的坐标,同理求出点N的坐标,求向量的坐标运算求出$\overrightarrow{BM}$、$\overrightarrow{BN}$的坐标,将B,M,N三点共线转化为$\overrightarrow{BM}$∥$\overrightarrow{BN}$,由共线向量的坐标条件列出方程,求出r的值.
解答 解:建立如图坐标系,不妨设正六边形ABCDEF的边AB=1,
则A(0,0),B(1,0),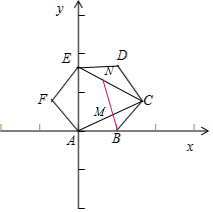 C($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
C($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
E(0,$\sqrt{3}$),
设M的坐标为(x,y),
∵$\frac{AM}{AC}=\frac{CN}{CE}=r$,∴(x,y)=r($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
则x=$\frac{3}{2}$r,y=$\frac{\sqrt{3}}{2}$r,即M($\frac{3}{2}$r,$\frac{\sqrt{3}}{2}$r),
同理可求,N的坐标是($\frac{3}{2}$(1-r),$\frac{\sqrt{3}}{2}$(1+r)),
∴$\overrightarrow{BM}$=($\frac{3}{2}$r-1,$\frac{\sqrt{3}}{2}$r),$\overrightarrow{BN}$=($\frac{1}{2}$-$\frac{3}{2}$r,(1+r)),
∵B,M,N三点共线,
∴$\overrightarrow{BM}$∥$\overrightarrow{BN}$,则($\frac{3}{2}$r-1)×$\frac{\sqrt{3}}{2}$(1+r)-$\frac{\sqrt{3}}{2}$r×($\frac{1}{2}$-$\frac{3}{2}$r)=0,
化简得,3r2=1,解得r=$\frac{{\sqrt{3}}}{3}$,
故答案为:$\frac{{\sqrt{3}}}{3}$.
点评 本题考查了利用坐标法解决向量的问题,向量的坐标运算,向量相等的条件,以及向量共线的坐标条件,考查方程思想,转化思想,建立恰当的坐标系是解题的关键.

| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{12},\frac{5π}{12}}]$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $[{0,\frac{π}{2}}]$ |
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{8}$ |
| 选修课程 | 线性代数 | 微积分 | 大学物理 | 商务英语 | 文学写作 | 合计 |
| 选课人数 | 180 | x | 120 | y | 60 | 600 |
(Ⅰ)从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(Ⅱ)从选出的10名学生中随机抽取3人,记ξ为选修线性代数人数与选择微积分人数差的绝对值.求随机变量ξ的分布列和数学期望.