题目内容
2.函数f(x)=(x+1)e-x(e为自然对数的底数)的单调减区间为(0,+∞).分析 先求出函数的导数,解关于导函数的不等式,求出函数的递减区间即可.
解答 解:∵f′(x)=(x+1)′•e-x+(x+1)(e-x)′
=e-x-(x+1)e-x
=-xe-x,
令f′(x)<0,解得:x>0,
∴f(x)在(0,+∞)递减,
故答案为:(0,+∞).
点评 本题考查了函数的单调性,考查了导数的应用,是一道基础题.

练习册系列答案
相关题目
13.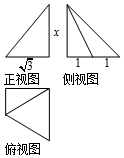 某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.
某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.
 某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.
某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.
11.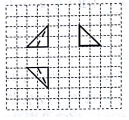 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |
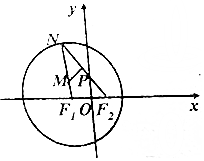 已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.
已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.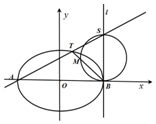 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.