题目内容
15.设θ是三角形的一个内角,$\overrightarrow m=({sinθ,cosθ}),\overrightarrow n=({1,1})$且$\overrightarrow m•\overrightarrow n=\frac{1}{3}$,则方程x2sinθ-y2cosθ=1表示的曲线是焦点在y轴上的椭圆(填抛物线、椭圆、双曲线的一种)分析 利用向量的数量积判断角的范围,推出方程表示的曲线即可.
解答 解:θ是三角形的一个内角,$\overrightarrow m=({sinθ,cosθ}),\overrightarrow n=({1,1})$且$\overrightarrow m•\overrightarrow n=\frac{1}{3}$,
可得sinθ+cosθ=$\frac{1}{3}$,即$\sqrt{2}$sin($θ+\frac{π}{4}$)=$\frac{1}{3}$,
可得$θ+\frac{π}{4}$∈($\frac{5π}{6}$,π),
θ∈($\frac{7π}{12}$,$\frac{3π}{4}$),sinθ>|cosθ|.
方程x2sinθ-y2cosθ=1表示的曲线是椭圆.
故答案为:y;椭圆.
点评 本题考查向量的数量积以及三角函数的化简求值,椭圆的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
5.若函数f(x)=ax2+bx+c,a>0,对任意实数x都有f(2+x)=f(2-x),那么( )
| A. | f(2)<f(1)<f(4) | B. | f(1)<f(2)<f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)<f(2)<f(1) |
4.函数f(x2)的定义域为(-3,1],则函数f(x-1)的定义域为( )
| A. | [2,10) | B. | [1,10) | C. | [1,2] | D. | [0,2] |
5.椭圆$\frac{x^2}{16}+\frac{y^2}{4}=1$上的一点A关于原点的对称点为B,F为它的右焦点,若AF⊥BF,则△AFB的面积是( )

| A. | 2 | B. | 4 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
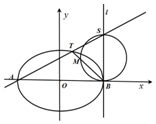 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.