题目内容
17.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为3x±4y=0,右焦点为(5,0),则双曲线C的方程为( )| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
分析 利用双曲线的渐近线方程推出a,b关系,通过右焦点坐标,求解a,b即可得到双曲线方程.
解答 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为3x±4y=0,可得4b=3a,右焦点为(5,0),可得c=5,则a2+b2=25,解得a=4,b=3,所求双曲线方程为:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1.
故选:D.
点评 本题考查双曲线的简单性质的应用,双曲线方程的求法,考查计算能力.

练习册系列答案
相关题目
7.已知函数$f(x)=lnx+\frac{1}{2}{x^2}-ax+1$,下列结论中错误的是( )
| A. | 当a=2时,x=1是f(x)的一个极值点 | B. | 当-2<a<2时,函数f(x)无极值 | ||
| C. | 当a>2时,f(x)的极小值小于0 | D. | ?a∈R,f(x)必有零点 |
8.圆O1:x2+y2-2x=0和圆O2:x2+y2-4x=0的公切线条数( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
5.若函数f(x)=ax2+bx+c,a>0,对任意实数x都有f(2+x)=f(2-x),那么( )
| A. | f(2)<f(1)<f(4) | B. | f(1)<f(2)<f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)<f(2)<f(1) |
2.已知抛物线C:y2=2px(p>0)过点(1,-2),经过焦点F的直线l与抛物线C交于A,B两点,A在x轴的上方,Q(-1,0),若以QF为直径的圆经过点B,则|AF|-|BF|=( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | 4 |
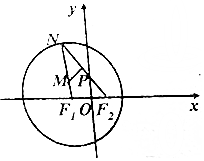 已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.
已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.