题目内容
16.某中学高二年级开设五门大学选修课程,其中属于数学学科的有两门,分别是线性代数和微积分,其余三门分别为大学物理、商务英语以及文学写作,年级要求每名学生只能选修其中一科,该校高二年级600名学生各科选课人数统计如下表:| 选修课程 | 线性代数 | 微积分 | 大学物理 | 商务英语 | 文学写作 | 合计 |
| 选课人数 | 180 | x | 120 | y | 60 | 600 |
(Ⅰ)从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(Ⅱ)从选出的10名学生中随机抽取3人,记ξ为选修线性代数人数与选择微积分人数差的绝对值.求随机变量ξ的分布列和数学期望.
分析 (Ⅰ)利用分层抽样求出各个选修人数,利用互斥事件的概率求解从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(Ⅱ)从选出的10名学生中随机抽取3人,记ξ为选修线性代数人数与选择微积分人数差的绝对值.求出ξ的可能值,就是概率,即可得到随机变量ξ的分布列和数学期望.
解答 解:因为选修数学学科人数所占总人数频率为0.6,即$\frac{180+x}{600}=0.6$,可得:x=180,又x+180+120+60+y=600,所以y=60,则根据分层抽样法:
抽取的10人中选修线性代数的人数为:10×$\frac{180}{600}$=3人;选修微积分的人数为:10×$\frac{180}{600}$=3人;选修大学物理的人数为:$10×\frac{120}{600}=2$人;选修商务英语的人数为:$10×\frac{60}{600}=1$人;选修文学写作的人数为:$10×\frac{60}{600}=1$人;
(Ⅰ)现从10人中选3人共有${C}_{10}^{3}=120$种选法,且每种选法可能性都相同,令事件A:选中的3人至少两人选修线性代数,事件B:选中的3人有两人选修线性代数,事件C:选中的3人都选修线性代数,且B,C为互斥事件,P(A)=P(B)+P(C)=$\frac{{C}_{3}^{2}×{C}_{7}^{1}}{{C}_{10}^{3}}$+$\frac{{C}_{3}^{3}}{{C}_{10}^{3}}$=$\frac{11}{60}$.
(Ⅱ)记X为3人中选修线性代数的代数,X的可能取值为0,1,2,3,记Y为3人中选修微积分的人数;Y的可能取值也为0,1,2,3,则随机变量ξ=|X-Y|的可能取值为0,1,2,3;
P(ξ=0)=P(X=0,Y=0)+P(X=1,Y=1)=$\frac{{C}_{4}^{3}}{{C}_{10}^{3}}+\frac{{C}_{3}^{1}{C}_{3}^{1}{C}_{4}^{1}}{{C}_{10}^{3}}=\frac{1}{3}$;
P(ξ=1)=P(X=0,Y=1)+P(X=1,Y=0)+P(X=1,Y=2)+P(X=2,Y=1)
=2×$\frac{{C}_{3}^{1}{C}_{4}^{2}}{{C}_{10}^{3}}+2×\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{10}^{3}}$=$\frac{9}{20}$,
P(ξ=2)=P(X=0,Y=2)+P(X=2,Y=0)=2×$\frac{{C}_{3}^{2}{C}_{4}^{1}}{{C}_{10}^{3}}$=$\frac{1}{5}$,
P(ξ=3)=P(X=0,Y=3)+P(X=3,Y=0)=2×$\frac{{C}_{3}^{3}}{{C}_{10}^{3}}$=$\frac{1}{60}$;
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{3}$ | $\frac{9}{20}$ | $\frac{1}{5}$ | $\frac{1}{60}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式和对立事件概率计算公式的合理运用.

| A. | [2,10) | B. | [1,10) | C. | [1,2] | D. | [0,2] |
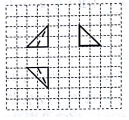 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |

| A. | 2 | B. | 4 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{13}}}{5}$ |